
【题目】如图,反比例函数![]() (k≠0)的图象经过点A(1,2)和B(2,n),
(k≠0)的图象经过点A(1,2)和B(2,n),
(1)以原点O为位似中心画出△A1B1O,使![]() =
=![]() ;
;
(2)在y轴上是否存在点P,使得PA+PB的值最小?若存在,求出P的坐标;若不存在,请说明理由.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
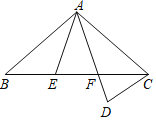
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚做游戏一个不透明的布袋里装有4个大小、质地均相同的乒乓球,球上分别标有数字1,2,3,4,随机从布袋中摸出一个乒乓球,记下数字后放回布袋里,再随机从布袋中摸出一个乒乓球,若这两个乒乓球上的数字之和能被4整除则小明赢;若两个乒乓球上的数字之和能被5整除则小刚赢;这个一个对游戏双方公平的游戏吗?请列表格或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
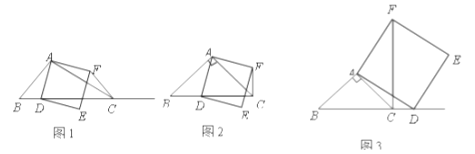
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园门票的收费标准如下:
门票类别 | 成人票 | 儿童票 | 团体票(限5张及以上) |
价格(元/人) | 100 | 40 | 60 |
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了( )元.
A.300B.260C.240D.220
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com