
【题目】如图,直线l1的解析表达式为y=- ![]() x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.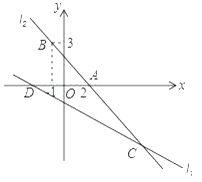
(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.
【答案】
(1)解:设l2的函数关系式为:y=kx+b,
∵直线过A(2,0),B(-1,3),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴l2的函数关系式为:y=-x+2
(2)解:∵l1的解析表达式为y=- ![]() x-1,
x-1,
∴D点坐标是(-2,0),
∵直线l1与l2交于点C.
∴ 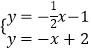 ,解得
,解得 ![]() ,
,
∴C(6,-4),
△ADC的面积为: ![]() ×AD×4=
×AD×4= ![]() ×4×4=8
×4×4=8
(3)解:∵△ADP与△ADC的面积相等,
∴△ADP的面积为8,
∵AD长是4,
∴P点纵坐标是4,
再根据P在l2上,则4=-x+2,解得:x=-2,
故P点坐标为:(-2,4)
【解析】(1)用待定系数法求出直线l2的函数关系式;
(2)先求出D点的坐标,然后解直线l1与l2的解析式组成的方程组,求出C点的坐标,然后利用面积公式计算出△ADC的面积;
(3)根据△ADP与△ADC的面积相等,得出AD的长,从而得出P点纵坐标是4,把P点的纵坐标代入l2得解析式,求出P点的横坐标,从而得出P点的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5小时后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
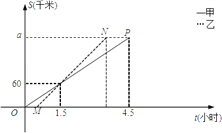
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )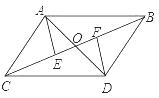
A.5对
B.6对
C.7对
D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a+2) ![]() -b+3=0,其中a、b为有理数,那么a= , b=;
-b+3=0,其中a、b为有理数,那么a= , b=;
(2)如果2b-a-(a+b-4) ![]() =5,其中a、b为有理数,求3a+2b的平方根.
=5,其中a、b为有理数,求3a+2b的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A. 8 B. 7或8 C. 6或7或8 D. 7或8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四组线段中,可以构成直角三角形的是( )
A.4cm、5cm、6cm
B.1cm、 ![]() cm、3cm
cm、3cm
C.2cm、3cm、4cm
D.1.5cm、2cm、2.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
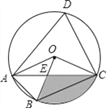
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2![]() ,则图中阴影部分面积是_____(结果保留π和根号)
,则图中阴影部分面积是_____(结果保留π和根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com