
【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为___________.

【答案】5
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角的性质可得∠B=∠BAD,再根据三角形内角和定理列式求出∠B=30°,设AB的垂直平分线与AB相交于点E,根据角平分线上的点到角的两边的距离相等可得DE=CD,根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2DE,然后根据BC=CD+BD列式计算即可得解.
如图,
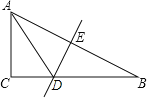
∵斜边AB的垂直平分线与BC相交于D点,
∴AD=BD,
∴∠B=∠BAD,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
∵∠C=90°,
∴∠B+∠BAD+∠CAD=90°,
即3∠B=90°,
∴∠B=30°,
∴BD=2DE,
∵BC=15,
∴CD+BD=DE+BD=DE+2DE=3DE=15,
∴DE=5,
即点D到斜边AB的距离为5.
故答案为:5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】探索:如图1,在![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() ;
;
发现:直角三角形中,如果有一个锐角等于![]() ,那么这个角所对的直角边等于斜边的_______.
,那么这个角所对的直角边等于斜边的_______.
应用:如图2,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 秒的速度向点
秒的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备添置一批计算机.
方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为![]() 、
、![]() 元.
元.
![]() 分别写出
分别写出![]() 、
、![]() 的函数关系式;
的函数关系式;
![]() 当学校添置多少台计算机时,两种方案的费用相同?
当学校添置多少台计算机时,两种方案的费用相同?
![]() 采用哪一种方案较省钱?说说你的理由.
采用哪一种方案较省钱?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若![]() ,则
,则![]() ;②直角三角形的两个锐角互余:③如果
;②直角三角形的两个锐角互余:③如果![]() ,那么
,那么![]() ④
④![]() 个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() .
.
(1)求方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解满足![]() 为非正数,
为非正数,![]() 为负数,求
为负数,求![]() 的取值范围:
的取值范围:
(3)在(2)的条件下,当![]() 为何整数时,不等式
为何整数时,不等式![]() 的解集为
的解集为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
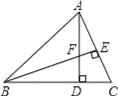
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A’,O’.设∠ABP=α.

(1)当α=10°时,∠ABA’= ____度;
(2)当点O’落在弧![]() 上时,求出α的度数.
上时,求出α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
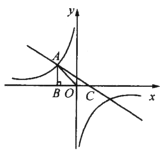
【题目】如图,已知反比例函数![]() (k<0)的图像经过点A(
(k<0)的图像经过点A(![]() ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com