
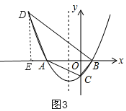
【题目】如图![]() ,已知抛物线
,已知抛物线![]() 与
与![]() 轴从左至右交于
轴从左至右交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 若抛物线过点
若抛物线过点![]() ,求抛物线的解析式;
,求抛物线的解析式;
![]() 在第二象限内的抛物线上是否存在点
在第二象限内的抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似?若存在,求
相似?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
![]() 如图
如图![]() ,在
,在![]() 的条件下,点
的条件下,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是抛物线上的点,在
是抛物线上的点,在![]() 轴上,从左至右有
轴上,从左至右有![]() 、
、![]() 两点,且
两点,且![]() ,问
,问![]() 在
在![]() 轴上移动到何处时,四边形
轴上移动到何处时,四边形![]() 的周长最小?请直接写出符合条件的点
的周长最小?请直接写出符合条件的点![]() 的坐标.
的坐标.
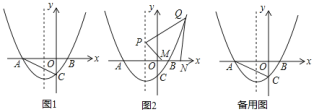
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将T点坐标代入函数解析式中即可求解a值;
(2)观察图1可知,∠ACB为钝角,则△ABD中只有∠DAB为钝角,故按照三角形相似的对应关系得∠DAB与∠ACB相对应,则可分下述两种对应情况分类讨论:①△DAB∽△BCA;②△DAB∽△ACB.两种情况下分别根据相似列出比例式进行求解;
(3)先代入Q点坐标求解t值,从而可求解出Q(6,10).由于四边形PQNM四边中,PQ和MN长度均已固定,因此只需要寻找PM+QN的最小值即可. 作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过
,过![]() 作
作![]() 轴,且
轴,且![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() ,交
,交![]() 轴于
轴于![]() ,则QG就是PM+QN的最小值.
,则QG就是PM+QN的最小值.
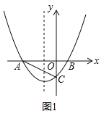
解:![]() 如图
如图![]() ,把
,把![]() 代入抛物线
代入抛物线![]() 得:
得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 、
、![]() ,
,
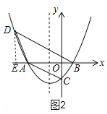
如图![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
设![]() ,
,
∵点![]() 在第二象限,
在第二象限,![]() 为钝角,
为钝角,
∴分两种情况:
①如图![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
![]() ,
,
则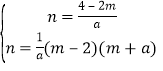 ,
,
解得:![]() 或
或![]() ,
,
∴![]() ,
,
由勾股定理得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]()
 ,
,
解得:![]() ,此方程无解;
,此方程无解;
②当![]() 时,如图
时,如图![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
有![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
则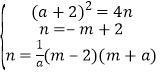 ,
,
解得: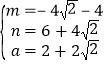 ,
,
则![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() ,
,
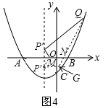
如图![]() ,作
,作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过
,过![]() 作
作![]() 轴,且
轴,且![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() ,交
,交![]() 轴于
轴于![]() ,
,
此时,![]() 就是
就是![]() 的最小值,由于
的最小值,由于![]() 、
、![]() 为定值,所以此时,四边形
为定值,所以此时,四边形![]() 的周长最小,
的周长最小,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 的解析式为:
的解析式为:![]() ,
,
把![]() 和
和![]() 代入得:
代入得:![]() ,
,
解得: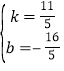 ,
,
∴![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,D、E分别是AB、AC的中点,延长BC至点F,使CF =![]() BC,连接DE、CD、EF.
BC,连接DE、CD、EF.

(1)求证:四边形DCFE是平行四边形;
(2)若等边三角形ABC的边长为a,写出求EF长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
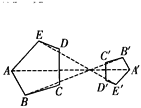
【题目】如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为2.如果五边形ABCDE的面积为16 cm2,周长为20 cm,那么五边形A'B'C'D'E'的面积为_______,周长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商准备进一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍.一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别是多少?
(2)若经销商购进A,B型商品共250件,试销A型商品售价为240元/件,B型商品售价为220元/件,且全部售出.已知购进B型商品m件,A型商品的件数不小于B型商品的件数,且B型商品的销量不小于80件,试求销售完这批商品的最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com