
【题目】已知二次函数![]() 的图象如图所示,有下列
的图象如图所示,有下列![]() 个结论:
个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,(
,(![]() 的实数);⑤
的实数);⑤![]() ,其中正确的结论有________.
,其中正确的结论有________.
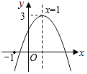
【答案】①③④⑤
【解析】
根据抛物线的对称轴可判断①;代入x=-1,结合图像可判断②;根据顶点坐标公式及图像中的顶点坐标可判断③;利用抛物线的最大值可判断④;根据抛物线与x轴交点的个数可判断⑤.
由图像知![]() =1,则
=1,则![]() ,①正确;
,①正确;
当x=-1时,y=a-b+c,由图像可知此时y<0,即a-b+c<0,则b>a+c,②错误;
由图可知顶点坐标为(1,3),则![]() ,即
,即![]() ,③正确;
,③正确;
当x=1时,y=a+b+c为最大值,当x=m时,y=am2+bm+c,由于m≠1,故a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),④正确;
由图可知,抛物线与x轴有两个交点,则b2-4ac>0,⑤正确;
故答案为:①③④⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.

(1)分别写出B、B'的坐标:B______;B′______;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②CE=AE;③△BDF≌△CDE; ④BF∥CE;⑤∠BAD=∠CAD.其中正确的有( ).

A.①⑤B.③⑤C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边
(1)若a=![]() ,c=4,求b
,c=4,求b
(2)若c=8,∠A=30°,求b
(3)若a:b=3:4,c=15,求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知抛物线
,已知抛物线![]() 与
与![]() 轴从左至右交于
轴从左至右交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 若抛物线过点
若抛物线过点![]() ,求抛物线的解析式;
,求抛物线的解析式;
![]() 在第二象限内的抛物线上是否存在点
在第二象限内的抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似?若存在,求
相似?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
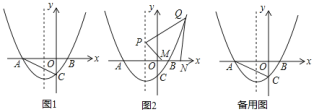
![]() 如图
如图![]() ,在
,在![]() 的条件下,点
的条件下,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是抛物线上的点,在
是抛物线上的点,在![]() 轴上,从左至右有
轴上,从左至右有![]() 、
、![]() 两点,且
两点,且![]() ,问
,问![]() 在
在![]() 轴上移动到何处时,四边形
轴上移动到何处时,四边形![]() 的周长最小?请直接写出符合条件的点
的周长最小?请直接写出符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C、O、A都不重合),过点A、C分别向直线BM作垂线段,垂足分别为E、F,连接OE,OF.


(1)①依据题意补全图形;
②猜想OE与OF的数量关系为_________________.
(2)小东通过观察、实验发现点M在射线CA上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明(1)中猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与△OAE全等的三角形,从而得到相等的线段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组△OAB和△EAB,再依据直角三角形斜边中线的性质,菱形四边相等,可以构造一对以OE和OF为对应边的全等三角形,即可证明猜想.
……
请你参考上面的想法,帮助小东证明(1)中的猜想(一种方法即可).
(3)当∠ADC=120°时,请直接写出线段CF,AE,EF之间的数量关系是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com