
【题目】如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3),
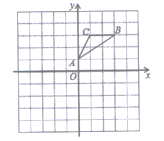
(1)①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出△ABC绕原点O逆时针旋转90°得到的△A2B2C2,写出点C2的坐标;
(2)若△ABC上任意一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则点Q的坐标为________.(用含m,n的式子表示)
【答案】(1)①见解析,②见解析,点C2的坐标为(-3,1);(2)(-n,m)
【解析】
(1)①根据关于原点对称的点的坐标特征得到A1、B1、C1的坐标,然后描点即可;
②利用网格特点和旋转的性质画出A、B、C的对应点A2、B2、C2,然后顺次连接,从而得到点C2的坐标;
(2)利用②中对应点的规律写出Q的坐标.
解:(1)①如图,△A1B1C1为所求;
②如图,△A2B2C2为所求,点C2的坐标为(-3,1)
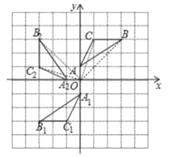
(2)∵A(0,1) 绕原点O逆时针旋转90°的对应点A2(-1,0),B(3,3) 绕原点O逆时针旋转90°的对应点B2(-3,3), C(1,3) 绕原点O逆时针旋转90°的对应点C2(-3,1),
∴点Q的坐标为(-n,m).


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.

(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
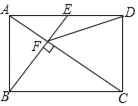
A. AF=![]() CF B. ∠DCF=∠DFC
CF B. ∠DCF=∠DFC
C. 图中与△AEF相似的三角形共有5个 D. tan∠CAD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
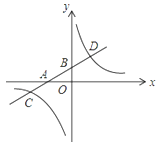
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=![]() 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(﹣6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(﹣6,﹣1),DE=3.
(1)求反比例函数与一次函数的解析式.
(2)根据图象直接回答:当x为何值时,一次函数的值小于反比例函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=-x2+bx+c的图像与x轴的交点为点A(3,0)和点B,与y轴交于点C(0,3),连接AC.
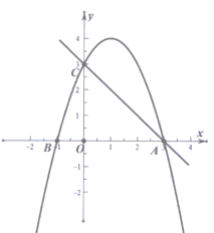
(1)求这个二次函数的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标及△ACD面积的最大值,若不存在,请说明理由.
(3)在抛物线上是否存在点E,使得△ACE是以AC为直角边的直角三角形如果存在,请直接写出点E的坐标即可;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)

(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
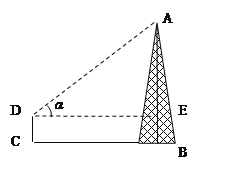
【题目】如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)
(参考数据:sin43° =0.6820, cos43° =0.7314, tan43° =0.9325
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com