
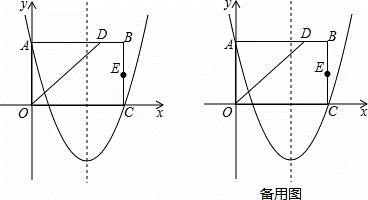
如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5, 0),二次函数y=
0),二次函数y= x2+bx+c的图象抛物线经过A,C两点.
x2+bx+c的图象抛物线经过A,C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴,y轴上的动点,顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
解答:
解:(1)将A(0,4)、C(5,0)代入二次函数y=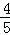 x2+bx+c,得
x2+bx+c,得
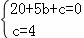 ,
,
解得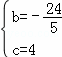 .
.
故二次函数的表达式y=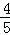 x2﹣
x2﹣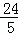 x+4;
x+4;
(2)如图:
延长EC至E′,使E′C=EC,延长DA至D′,使D′A=DA,连接D′E′,交x轴于F点,交y轴于G点,
GD=GD′EF=E′F,
(DG+GF+EF+ED)最小=D′E′+DE,
由E点坐标为(5,2),D(4,4),得D′(﹣4,4),E(5,﹣2).
由勾股定理,得
DE=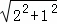 =
=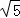 ,D′E′=
,D′E′=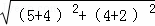 =
=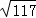 ,
,
(DG+GF+EF+ED)最小=D′E′+DE=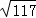 +
+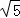 ;
;
(3)如下图:
OD= .
.
∵S△ODP的面积=12,
∴点P到OD的距离=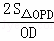 =3
=3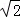 .
.
过点O作OF⊥OD,取OF=3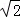 ,过点F作直线FG∥OD,交抛物线与点P1,P2,
,过点F作直线FG∥OD,交抛物线与点P1,P2,

在Et△OGF中,OG=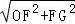 =
=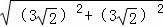 =6,
=6,
∴直线GF的解析式为y=x﹣6.
将y=x﹣6代入y=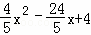 得:x﹣6=
得:x﹣6=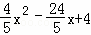 ,
,
解得: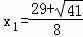 ,
,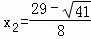 ,
,
将x1、x2的值代入y=x﹣6得:y1=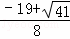 ,y2=
,y2=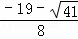
∴点P1(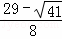 ,
,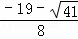 ),P2(
),P2(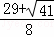 ,
,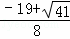 )
)
如下图所示:
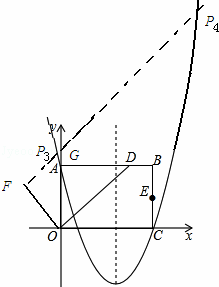
过点O作OF⊥OD,取OF=3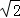 ,过点F作直线FG交抛物线与P3,P4,
,过点F作直线FG交抛物线与P3,P4,
在Rt△PFO中,OG=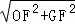 =6
=6
∴直线FG的解析式为y=x+6,
将y=x+6代入y=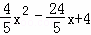 得:x+6=
得:x+6=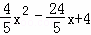
解得: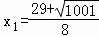 ,
,
y1=x1+6=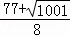 ,y2=x2+6=
,y2=x2+6=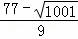
∴p3(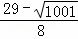 ,
,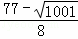 ),p4(
),p4(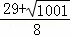 ,
,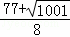 )
)
综上所述:点P的坐标为:(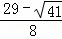 ,
,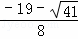 )或(
)或(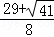 ,
,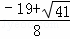 )或(
)或(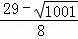 ,
,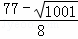 )或(
)或(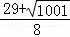 ,
,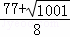 ).
).

点评:
本题主要考查的是二次函数的综合应用,求得点P到OD的距离是解题的关键,解得此类问题通常可以将函数问题转化为方程或方程组的问题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
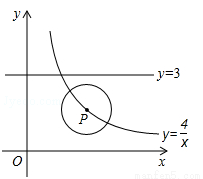
如图,P是双曲线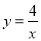 (x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 .
(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调査,如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,则每件童装应降价多少元?设每件童裝应降价x元,可列方程为
查看答案和解析>>
科目:初中数学 来源: 题型:
学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣ ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )
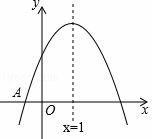
A. ①③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
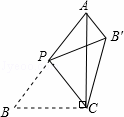
如图,在△ABC中,∠ACB=90°,AB= 5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com