
分析 设a2+b2=k③,先将原方程相加后得方程④,③与④组成新的方程组,分别相加或相减得出关于k的不等式,三个不等式组成不等式组解出即可.
解答 解:$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}={4}^{2}①}\\{{b}^{2}+{c}^{2}={5}^{2}②}\end{array}\right.$,
设a2+b2=k③,
由②-①得:b2-a2=52-42=9④,
则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=k③}\\{{b}^{2}-{a}^{2}=9④}\end{array}\right.$,
③-④得:2a2=k-9,
a2=$\frac{k-9}{2}$>0,
③+④得:2b2=k+9,
b2=$\frac{k+9}{2}$>0,
①+②得:a2+b2+2c2=42+52,
k+2c2=41,
c2=$\frac{41-k}{2}$>0,
得:9<k<41,
即a2+b2的取值为:9<a2+b2<41.
点评 本题是求高次方程的取值问题,考查了根据方程的特点进行加减消元及不等式组的解法,有一定的技巧性.


科目:初中数学 来源: 题型:选择题
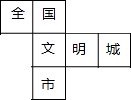 在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )
在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )| A. | 全 | B. | 国 | C. | 明 | D. | 城 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 △ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.
△ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com