
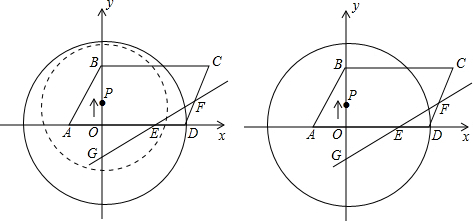
���� ��1�������P�������ֻ����ø�Բ�İ뾶���ɣ���P��ֱ��EG���У���PH��EG��H����PH=6-t��P��0��2t����������������Rt��PHG��Rt��EOG�Ķ�Ӧ�߳ɱ����õ�$\frac{6-t}{4}$=$\frac{2t+3}{5}$���ɴ����t��ֵ�������õ���Բ�İ뾶������Բ�������ʽ��ɣ�
��2����y=$\sqrt{3}$x+3$\sqrt{3}$�������A��-3��0����B��0��3$\sqrt{3}$�������ƽ���ı��ε����ʵõ�C��9��3$\sqrt{3}$������������ǵ����Ǻ���ֵ��֪��A=60�㣮���õȱ������ε������ã�Q1��3��3$\sqrt{3}$����Q2��12��0������ȻQ2��12��0���������ڡ�P�ڣ���Q1��3��3$\sqrt{3}$���ڡ�P�ڣ���ɵã�PQ1��r���뾶�����ɴ����t��ȡֵ��Χ��
��� 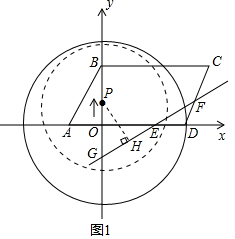 �⣺��1������y=$\frac{3}{4}$x+mͼ�����E��4��0����
�⣺��1������y=$\frac{3}{4}$x+mͼ�����E��4��0����
��m=-3��G��0��-3����
��P��ֱ��EG���У���PH��EG��H����ͼ1��
��PH=6-t��P��0��2t����
��Rt��PHG��Rt��EOG�ɵã�$\frac{PH}{OE}$=$\frac{PG}{GE}$����$\frac{6-t}{4}$=$\frac{2t+3}{5}$��
���t=$\frac{18}{13}$��
���ԡ�P�뾶Ϊ6-$\frac{18}{13}$=$\frac{60}{13}$��
��P���Ϊ����•��$\frac{60}{13}$��2=$\frac{3600}{169}$�У�
��2����ͼ2����y=$\sqrt{3}$x+3$\sqrt{3}$ͼ����x�ᡢy��ֱ���A��B��
��A��-3��0����B��0��3$\sqrt{3}$����C��9��3$\sqrt{3}$����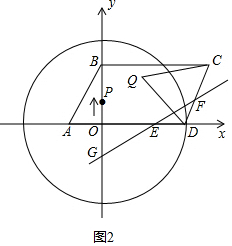
��tanA=$\frac{OB}{OA}$=$\sqrt{3}$��
���A=60�㣮
��CDΪ�����ȱ�������CDQ����D=��A=60�㣬CD=AB=6��
��Q1��3��3$\sqrt{3}$����Q2��12��0����
��ȻQ2��12��0���������ڡ�P�ڣ�
��Q1��3��3$\sqrt{3}$���ڡ�P�ڣ���ɵã�PQ1��r���뾶����
��P��0��2t����r=6-t��
����9+��2t-3$\sqrt{3}$��2����6-t��2��t2-��4$\sqrt{3}$-4��t��0��
��t��0��
��t-��4$\sqrt{3}$-4����0
��t��4��$\sqrt{3}$-1����
��t��ȡֵ��ΧΪ0��t��4��$\sqrt{3}$-1����
���� ���⿼����һ�κ����ۺ��⣬�ۺ������˴���ϵ������һ�κ�������ʽ��Բ�����ߵ����ʣ�����Բ��λ�ù�ϵ�����������ε��ж������ʣ�����ʽ�Ľⷨ��֪ʶ�㣬�ѶȽϴ�


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
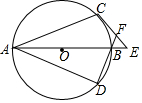 ��ͼ��ABΪ��O��ֱ����AC��ADΪ��O���ң�$\widehat{BC}$=$\widehat{BD}$����C����O�����߽�AB���ӳ�����E��DB���ӳ��߽�CE��F������O�İ뾶Ϊ3����E=45�㣬��CF�ij�Ϊ6-3$\sqrt{2}$��
��ͼ��ABΪ��O��ֱ����AC��ADΪ��O���ң�$\widehat{BC}$=$\widehat{BD}$����C����O�����߽�AB���ӳ�����E��DB���ӳ��߽�CE��F������O�İ뾶Ϊ3����E=45�㣬��CF�ij�Ϊ6-3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��һС������ͼ��ʾ���������������������ABCD�߳�Ϊ3��E��F��G��H�ֱ�Ϊ�����ϵĵ㣬��AE=BF=CG=DH=1����С��ֹͣ������������Ӱ����ĸ�����$\frac{5}{9}$��
��֪��һС������ͼ��ʾ���������������������ABCD�߳�Ϊ3��E��F��G��H�ֱ�Ϊ�����ϵĵ㣬��AE=BF=CG=DH=1����С��ֹͣ������������Ӱ����ĸ�����$\frac{5}{9}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
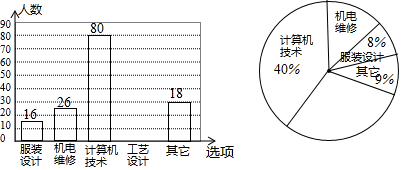
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | 2 | D�� | 2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
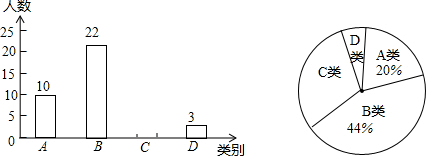
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
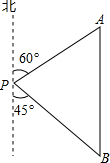 ��һ�ڼ䣬С���������Ļ�ɽ�μ����ʵ������ھ���P����þ���Bλ����ƫ��45�㷽��Ȼ���ر�ƫ��60�㷽����100���ᄚ��A����ʱ��þ���B����λ�ھ���A�����Ϸ�����A��B֮��ľ��룮���ο����ݣ�$\sqrt{3}$��1.732�������ȷ��0.1�ף�
��һ�ڼ䣬С���������Ļ�ɽ�μ����ʵ������ھ���P����þ���Bλ����ƫ��45�㷽��Ȼ���ر�ƫ��60�㷽����100���ᄚ��A����ʱ��þ���B����λ�ھ���A�����Ϸ�����A��B֮��ľ��룮���ο����ݣ�$\sqrt{3}$��1.732�������ȷ��0.1�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | $\frac{3}{10}$ | C�� | $\frac{1}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com