
【题目】如图,![]() 中,
中,![]() 且
且![]() 是
是![]() 的中点
的中点
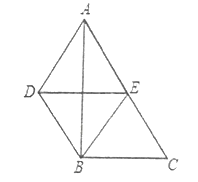
(1)求证:四边形![]() 是平行四边形。
是平行四边形。
(2)求证:四边形![]() 是菱形。
是菱形。
(3)如果![]() 时,求四边形ADBE的面积
时,求四边形ADBE的面积
(4)当![]() 度时,四边形
度时,四边形![]() 是正方形(不证明)
是正方形(不证明)
【答案】(1)见解析;(2)见解析;(3)24;(4)45.
【解析】
(1)推出CE=BD,CE∥BD,可证四边形![]() 是平行四边形;
是平行四边形;
(2)求出BDF=AE,BD∥AE,得出平行四边形ADBE,根据DE∥BC,∠ABC=90°推出DE⊥AB,根据菱形的判定推出即可;
(3)由四边形BDEC是平行四边形,可得DE=BC=6,然后根据菱形的面积公式求解即可;
(4)当![]() 45度时,可证△ABC是等腰直角三角形,从而AB=BC=DE,可证四边形
45度时,可证△ABC是等腰直角三角形,从而AB=BC=DE,可证四边形![]() 是正方形.
是正方形.
(1)证明:∵E是AC的中点,
∴CE=AE=![]() AC,
AC,
∵DB=![]() AC,
AC,
∵BD=CE,
∵BD∥AC,
∴BD∥CE,
∴四边形BDEC是平行四边形,
∴DE∥BC.
(2)证明:∵DE∥BC,∠ABC=90°,
∴DE⊥AB,
∵AE=![]() AC,DB=
AC,DB=![]() AC,BD∥AC,
AC,BD∥AC,
∴BD=AE,BD∥AE,
∴四边形ADBE是平行四边形,
∴平行四边形ADBE是菱形;
(3)∵四边形BDEC是平行四边形,
∴DE=BC=6.
∵四边形ADBE是菱形,
∴四边形ADBE面积=![]() ;
;
(4)当![]() 45度时,四边形
45度时,四边形![]() 是正方形.
是正方形.
∵![]() 45,
45,
∴△ABC是等腰直角三角形,
∴AB=BC=DE,
∵四边形ADBE是菱形,
∴四边形![]() 是正方形.
是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计307元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为P元,试写出P与x之间的函数关系式,并写出自变量x的取值范围.
(2)李经理将这批野生茵存放多少天后出售可获得最大利润W元?(利润=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①![]() 是单项式;②几个数相乘,积的符号由负因数的个数决定,当负因数的个数是偶数个时积为正;③若x=﹣1是方程3x﹣m=0的解,则m=3;④1﹣(ab+1)2的最大值为1;⑤长方形硬纸片绕它的一边旋转,形成一个圆柱体,这可以说面动成体.其中正确说法的序号是_____.
是单项式;②几个数相乘,积的符号由负因数的个数决定,当负因数的个数是偶数个时积为正;③若x=﹣1是方程3x﹣m=0的解,则m=3;④1﹣(ab+1)2的最大值为1;⑤长方形硬纸片绕它的一边旋转,形成一个圆柱体,这可以说面动成体.其中正确说法的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
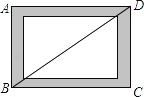
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
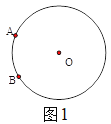
理解:(1)如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
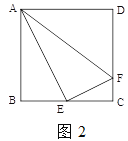
(2)如图![]() ,在正方形
,在正方形![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
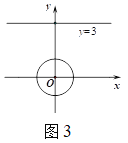
运用:(3)如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
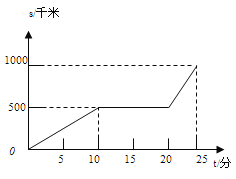
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com