
【题目】电子政务、数字经济、智慧社会一场数字革命正在神州大地激荡.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ,D组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.

【答案】(1)20、32、28.8;(2)①恰好1名男生和1名女生被抽取参加5G体验活动的概率为![]() ;②至少1名女生被抽取参加5G体验活动的概率为
;②至少1名女生被抽取参加5G体验活动的概率为![]() .
.
【解析】
(1)先根据A组人数及其所占百分比求出总人数,由各组人数之和等于总人数求出B组人数m的值,用360°乘以D组人数所占比例可得;
(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
(1)被调查的总人数为10÷20%=50,
则m=50﹣(10+16+4)=20,
n%![]() 100%=32%,即n=32,
100%=32%,即n=32,
D组的圆心角是360°![]() 28.8°,
28.8°,
故答案为:20、32、28.8;
(2)①设男同学标记为A、B;女学生标记为1、2,可能出现的所有结果列表如下:
A | B | 1 | 2 | |
A | / | (B,A) | (1,A) | (2,A) |
B | (A,B) | / | (1,B) | (2,B) |
1 | (A,1) | (B,1) | / | (2,1) |
2 | (A,2) | (B,2) | (1,2) | / |
共有 12 种可能的结果,且每种的可能性相同,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为![]() ;
;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
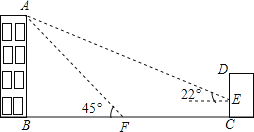
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
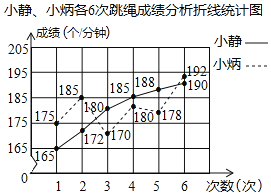
【题目】体育老师要从每班选取一名同学,参加学校的跳绳比赛.小静和小炳是跳绳能手,下面分别是小静、小炳各6次跳绳成绩统计图和成绩分析表
小静、小炳各6次跳绳成绩分析表
成绩 姓名 | 平均数 | 中位数 | 方差 |
小静 | 180 | 182.5 | 79.7 |
小炳 | 180 | a | 33 |
(1)根据统计图的数据,计算成绩分析表中a= ;
(2)结合以上信息,请你从两个不同角度评价这两位学生的跳绳水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() .
.
(1)如图1,若二次函数图象也经过点![]() ,试求出该二次函数解析式,并求出
,试求出该二次函数解析式,并求出![]() 的值.
的值.
(2)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
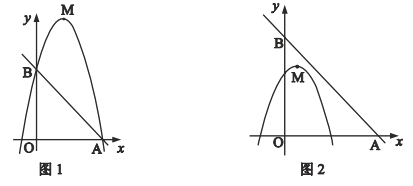
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校数学兴趣小组利用机器人开展数学活动.在相距![]() 个单位长度的直线跑道
个单位长度的直线跑道![]() 上,机器人甲从端点
上,机器人甲从端点![]() 出发,匀速往返于端点
出发,匀速往返于端点![]() 、
、![]() 之间,机器人乙同时从端点
之间,机器人乙同时从端点![]() 出发,以大于甲的速度匀速往返于端点
出发,以大于甲的速度匀速往返于端点![]() 、
、![]() 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
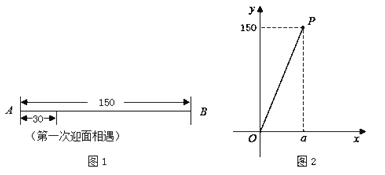
(观察)
①观察图![]() ,若这两个机器人第一次迎面相遇时,相遇地点与点
,若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第二次迎面相遇时,相遇地点与点
个单位长度,他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.兴趣小组成员发现了
个单位长度.兴趣小组成员发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图
,如图![]() 所示).
所示).
①![]() = _____;
= _____;
②分别求出各部分图象对应的函数表达式,并在图![]() 中补全函数图象;
中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第三次迎面相遇时,相遇地点与点
个单位长度,他们第三次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点
个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 不超过
不超过![]() 个单位长度,则他们第一次迎面相遇时,相遇地点与点
个单位长度,则他们第一次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 的取值范围是 _____.(直接写出结果)
的取值范围是 _____.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
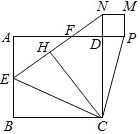
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 的中点,点
的中点,点![]() 与
与![]() 关于
关于![]() 对称,
对称,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 在
在![]() 的延长线上,作正方形
的延长线上,作正方形![]() ,连接
,连接![]() ,记正方形
,记正方形![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
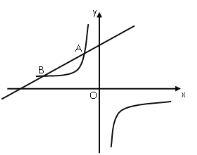
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
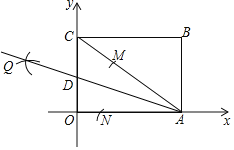
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于![]() MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com