
【题目】如图,在△ABC中,![]() .以AC为直径的
.以AC为直径的![]() O交AB于点D,交BC于点E.
O交AB于点D,交BC于点E.
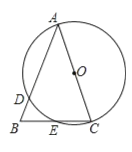
(1)求证:弧DE=弧CE.
(2)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连结AE,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE,进而利用等腰三角形的性质得出∠BAE=∠CAE,进而证明即可;
(2)连结DE,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.
(1)连结AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE,
∴∠BAE=∠CAE,
∴弧DE=弧CE.;
(2)连结DE,CD,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴△BED∽△BAC,
∴![]() ,,即
,,即![]() ,
,
∴BA=9,
∴AC=BA=9.
∴AD=ABBD=92=7,
∴DC=![]() =4
=4![]()
∴tan∠BAC=![]() =
=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
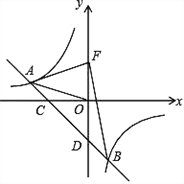
【题目】如图,一次函数 yax 2(a0) 的图象与反比例函数 y![]() (k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=
(k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=![]() ,AO=
,AO=![]() .
.
(1)求这个一次函数和反比例函数的解析式;
(2) 若点 F 是点D 关于 x 轴的对称点,求△ABF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州西山漾湿地公园一休闲草坪上有一架秋千.秋千静止时,底端A到地面的距离AB为0.5m,从竖直位置开始,向右可摆动的最大夹角为37°,若秋千的长OA=2m.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
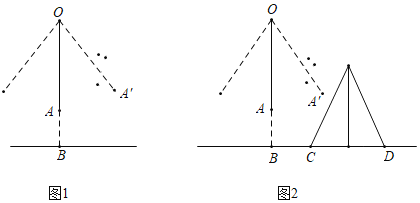
(1)如图1,当向右摆动到最大夹角时,求A'到地面的距离;
(2)如图2,若有人在B点右侧搭建了一个等腰三角形帐篷,已知BC=0.6m,CD=2m,帐篷的高为1.8m,当人站立在秋千上,请问摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?
查看答案和解析>>
科目:初中数学 来源: 题型:
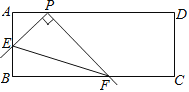
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形

ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在
一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀
后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1
个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法
求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节吃月饼是中华民族的传统习族.据了解,甲厂家生产了![]() 三个品种的盒装月饼,乙厂家生产了
三个品种的盒装月饼,乙厂家生产了![]() 三个品种的盒装月饼.中秋节前,某商场在甲、乙两个厂家中各选购一个品种的盒装月饼销售,并用画树状图的方法得出所有可能的选购方案。如图是商场一位部门经理所画的正确树状图的一部分.
三个品种的盒装月饼.中秋节前,某商场在甲、乙两个厂家中各选购一个品种的盒装月饼销售,并用画树状图的方法得出所有可能的选购方案。如图是商场一位部门经理所画的正确树状图的一部分.
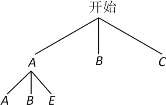
(1)请补全部门经理所画的树状图;
(2)求商场选购到不同品种的盒装月饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB与x轴、y轴分别交于点A、B,作等腰直角三角形ABC,使∠BAC=90°,将△ABC沿着射线AB平移得到△A′B′C′,当点A′与点B重合时停止运动.设平移距离为m,△A′B′C′与△ABO重合部分的面积为S,S关于m的函数图象如图2所示.(其中0≤m≤![]() 时,函数的解析式不同)
时,函数的解析式不同)
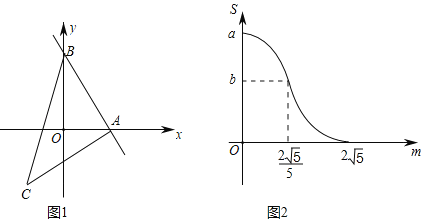
(1)填空:a= ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com