
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпABгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌзїЕШбќжБНЧШ§НЧаЮABCЃЌЪЙЁЯBACЃН90ЁуЃЌНЋЁїABCбизХЩфЯпABЦНвЦЕУЕНЁїAЁфBЁфCЁфЃЌЕБЕуAЁфгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЎЩшЦНвЦОрРыЮЊmЃЌЁїAЁфBЁфCЁфгыЁїABOжиКЯВПЗжЕФУцЛ§ЮЊSЃЌSЙигкmЕФКЏЪ§ЭМЯѓШчЭМ2ЫљЪОЃЎЃЈЦфжа0ЁмmЁм![]() ЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
ЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
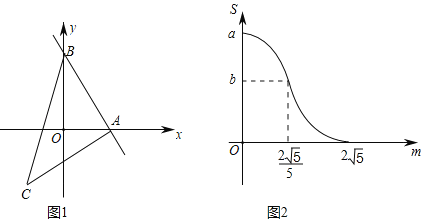
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЧѓSЙигкmЕФНтЮіЪНЃЌВЂаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ10ЃЛЃЈ2ЃЉyЃНЉ![]() x+4ЃЛЃЈ3ЃЉSЃН
x+4ЃЛЃЈ3ЃЉSЃН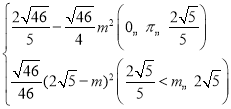 ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭМаЮЦНвЦОрРыm=AB=![]() ЃЌЕБm=0ЪБЭМЯѓЕФУцЛ§МДЪЧШ§НЧаЮABCЕФУцЛ§ЃЌгЩДЫМДПЩЧѓГіaЕФжЕЃЛ
ЃЌЕБm=0ЪБЭМЯѓЕФУцЛ§МДЪЧШ§НЧаЮABCЕФУцЛ§ЃЌгЩДЫМДПЩЧѓГіaЕФжЕЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЗЂЩњБфЛЏЪБЪЧжБЯпACЙ§ЕуOЃЌгЩДЫЕУЕНHAЃНmЃН![]() ЃЌдйЧѓГіBHЃЌИљОнЩфгАЖЈРэЧѓГіOAЃЌдйЧѓГіOBЃЌЕУЕНЕуAЁЂBЕФзјБъМДПЩЧѓГіжБЯпABЕФНтЮіЪНЃЛ
ЃЌдйЧѓГіBHЃЌИљОнЩфгАЖЈРэЧѓГіOAЃЌдйЧѓГіOBЃЌЕУЕНЕуAЁЂBЕФзјБъМДПЩЧѓГіжБЯпABЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЂйЕБ0ЁмmЁм![]() ЪБЃЌЂкЕБ
ЪБЃЌЂкЕБ![]() ЃМmЁм
ЃМmЁм![]() ЪБЃЌЧѓSЙигкmЕФНтЮіЪН
ЪБЃЌЧѓSЙигкmЕФНтЮіЪН
ЃЈ1ЃЉДгЭМ2ПЩЕУЃКABЃН2![]() ЃЌ
ЃЌ
mЃН0ЪБЃЌЭМЯѓУЛгаЦНвЦЃЌдђДЫЪБaЃНSЁїABCЃН![]() AB2ЃН10ЃЌ
AB2ЃН10ЃЌ
ЙЪД№АИЮЊЃК10ЃЛ
ЃЈ2ЃЉЙ§ЕуOзї![]() ЃЌ
ЃЌ
ЕББпACЙ§ЕуOЪБЃЌSЕФБэДяЪНЗЂЩњБфЛЏЃЌДЫЪББпACвЦЖЏЕНHCЁфЫљДІЕФЮЛжУЃЌ

дђHAЃНmЃН![]() ЃЌBHЃНABЉAHЃН
ЃЌBHЃНABЉAHЃН![]() ЃЌ
ЃЌ
ЖјOH2ЃНHAHBЃН![]() ЃЌдђOAЃН2ЃЌ
ЃЌдђOAЃН2ЃЌ
ЖјAB2ЃН20ЃЌЙЪOBЃН4ЃЌдђЕуAЁЂBЕФзјБъЗжБ№ЮЊЃКЃЈ2ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЌ
НЋЕуAЁЂBЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК
жБЯпABЕФБэДяЪНЮЊЃКyЃНЉ![]() x+4ЃЛ
x+4ЃЛ
ЃЈ3ЃЉЂйЕБ0ЁмmЁм![]() ЪБЃЌ
ЪБЃЌ
ШчЭМ1зѓЭМЫљЪОЃЌЩшБпAЁфCЁфНЛxжсгкЕуHЃЌ
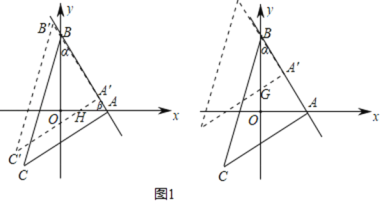
дђAЁфHЃНAAЁфtanІТЃЌ
SЃНSЫФБпаЮBAЁфHOЃНSЁїABOЉSЁїAAЁфHЃН![]() OAЁСOBЉ
OAЁСOBЉ![]() AЁфAЁСAЁфHЃН
AЁфAЁСAЁфHЃН![]()
![]() ЁСm2ЁС
ЁСm2ЁС![]() ЃН
ЃН![]() Љ
Љ![]() m2ЃЌ
m2ЃЌ
ЕБmЃН![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃНbЃЌ
ЃНbЃЌ
ЂкЕБ![]() ЃМmЁм
ЃМmЁм![]() ЪБЃЌ
ЪБЃЌ
ШчЭМ1гвЭМЫљЪОЃЌЩшБпAЁфCЁфНЛyжсгкЕуGЃЌ
SЃНSЁїAЁфBGЃН![]() ЁСAЁфBЁСAЁфGЃН
ЁСAЁфBЁСAЁфGЃН![]() ЁСABЁф2ЁСtanІСЃН
ЁСABЁф2ЁСtanІСЃН![]() ЁСЃЈ
ЁСЃЈ![]() ЉmЃЉ2ЃН
ЉmЃЉ2ЃН![]() ЃЈ
ЃЈ![]() ЉmЃЉ2ЃЛ
ЉmЃЉ2ЃЛ
злЩЯЃЌSЃН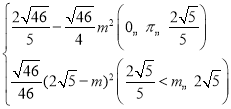 .
.


 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌ![]() .вдACЮЊжБОЖЕФ
.вдACЮЊжБОЖЕФ![]() OНЛABгкЕуDЃЌНЛBCгкЕуE.
OНЛABгкЕуDЃЌНЛBCгкЕуE.
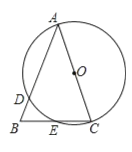
ЃЈ1ЃЉЧѓжЄЃКЛЁDE=ЛЁCE.
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
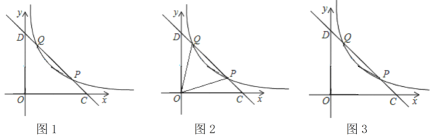
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌКЏЪ§![]() ЃЈmЮЊГЃЪ§ЃЌmЃО1ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ЕуPЃЈmЃЌ1ЃЉКЭQЃЈ1ЃЌmЃЉЃЌжБЯпPQгыxжсЃЌyжсЗжБ№НЛгкCЃЌDСНЕу.
ЃЈmЮЊГЃЪ§ЃЌmЃО1ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ЕуPЃЈmЃЌ1ЃЉКЭQЃЈ1ЃЌmЃЉЃЌжБЯпPQгыxжсЃЌyжсЗжБ№НЛгкCЃЌDСНЕу.
ЃЈ1ЃЉЧѓЁЯOCDЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгOQЁЂOPЃЌЕБЁЯDOQ=ЁЯOCD-ЁЯPOCЪБЃЌЧѓДЫЪБmЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуAЃЌЕуBЗжБ№дкxжсКЭyжсе§АыжсЩЯЕФЖЏЕу.дйвдOAЁЂOBЮЊСкБпзїОиаЮOAMB.ШєЕуMЧЁКУдкКЏЪ§![]() ЃЈmЮЊГЃЪ§ЃЌmЃО1ЃЌxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧвЫФБпаЮBAPQЮЊЦНааЫФБпаЮЃЌЧѓДЫЪБOAЁЂOBЕФГЄЖШ.
ЃЈmЮЊГЃЪ§ЃЌmЃО1ЃЌxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧвЫФБпаЮBAPQЮЊЦНааЫФБпаЮЃЌЧѓДЫЪБOAЁЂOBЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
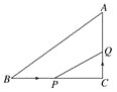
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌBCЃН16 cmЃЌACЃН12 cmЃЌЕуPДгЕуBГіЗЂЃЌбиBCвд2 cm/sЕФЫйЖШЯђЕуCвЦЖЏЃЌЕуQДгЕуCГіЗЂЃЌвд1 cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌШєЕуPЁЂQЗжБ№ДгЕуBЁЂCЭЌЪБГіЗЂЃЌЩшдЫЖЏЪБМфЮЊtsЃЌЕБtЃН__________ЪБЃЌЁїCPQгыЁїCBAЯрЫЦЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЬНОП
ШчЭМЃЌХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы
ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы![]() жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ
жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ![]() .СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
.СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ЁїBCDЕФУцЛ§ЕШгкЁїAOCЕФУцЛ§ЕФ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌШєЕуMЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН6ЃЌADЃН8ЃЌЕуEЪЧБпADЩЯЕФвЛИіЖЏЕуЃЌАбЁїBAEбиBEелЕўЃЌЕуAТфдкAЁфДІЃЌШчЙћAЁфЧЁдкОиаЮЕФЖдНЧЯпЩЯЃЌдђAEЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
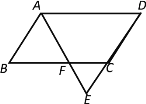
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌAB=3ЃЌAD=5ЃЌAEЦНЗжЁЯBADЃЌНЛBCгкFЃЌНЛDCбгГЄЯпгкEЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌЁЯCЃН90ЁуЃЌABЃН1ЃЌtanAЃН![]() ЃЌЙ§ABБпЩЯвЛЕуPзїPEЁЭACгкEЃЌPFЁЭBCгкFЃЌEЁЂFЪЧДЙзуЃЌдђEFЕФзюаЁжЕЕШгк_____ЃЎ
ЃЌЙ§ABБпЩЯвЛЕуPзїPEЁЭACгкEЃЌPFЁЭBCгкFЃЌEЁЂFЪЧДЙзуЃЌдђEFЕФзюаЁжЕЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
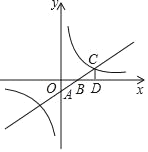
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓгызјБъжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓдкЕквЛЯѓЯоЕФНЛЕуЮЊCЃЌCDЁЭxжсгкDЃЌШєOBЃН3ЃЌODЃН6ЃЌЁїAOBЕФУцЛ§ЮЊ3ЃЎ
ЕФЭМЯѓдкЕквЛЯѓЯоЕФНЛЕуЮЊCЃЌCDЁЭxжсгкDЃЌШєOBЃН3ЃЌODЃН6ЃЌЁїAOBЕФУцЛ§ЮЊ3ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБxЃО0ЪБЃЌБШНЯkx+bгы![]() ЕФДѓаЁЃЎ
ЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com