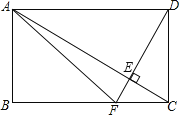
【题目】如图，在矩形ABCD中，∠ACB＝30°，过点D作DE⊥AC于点E，延长DE交BC于点F，连接AF，若AF＝
，线段DE的长为_____．
【答案】
．
【解析】
由直角三角形的性质得出CD＝
CF，设CF＝x，则AB＝x，BC＝3x，则BF=2x，利用勾股定理求出x，再证明△ADE∽△CFE，然后理由相似的性质求出CD即可.
解：∵四边形ABCD是矩形，
∴AD∥BC，∠ADC＝∠B＝∠BCD＝90°，AB＝CD，AD＝BC，AD∥BC，
∴∠DAC＝∠ACB＝30°，
∴AD＝CD，∠DCE＝60°，
∵DF⊥AC，
∴EF＝
CF，∠CDF＝30°，
∴CD＝CF，
设CF＝x，则AB＝CD＝x，BC＝AD＝CD＝3x，
∴BF＝BC﹣CF＝3x﹣x＝2x，
在Rt△ABF中，由勾股定理得：（x）2+（2x）2＝（
）2，
解得：x＝，
∴CF＝，EF＝
，AD＝3，
∵AD∥BC，
∴△ADE∽△CFE，
∴
＝
，即
＝
，
∴DE＝；
故答案为：．
每课必练系列答案科目：初中数学 来源： 题型：
【题目】设中学生体质健康综合评定成绩为
分，满分为100分，规定：
为
级；
为
级；
为
级；x<60为D级．现随机抽取某中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：
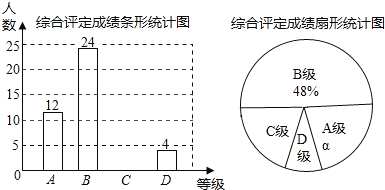
（1）在这次调查中，一共抽取了 名学生，级人数占本次抽取人数的百分比为 
；
（2）扇形统计图中级对应的圆心角为 度；
（3）若该校共有1000名学生，请你估计该校
级学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，AC=8，sin A=
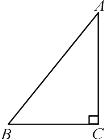
(1)求AB的长;
(2)若点E在Rt△ABC的直角边上，点F在斜边AB上，当△CFE∽△ABC时，求CE的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某翻译团为成为2022年冬奥会志愿者做准备，该翻译团一共有五名翻译，其中一名只会翻译西班牙语，三名只会翻译英语，还有一名两种语言都会翻译．
（1）求从这五名翻译中随机挑选一名会翻译英语的概率；
（2）若从这五名翻译中随机挑选两名组成一组，请用树状图或列表的方法求该纽能够翻译上述两种语言的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2．
（1）求k的取值范围；
（2）如果x1+x2﹣x1x2＜﹣1且k为整数，求k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：
（1）本次一共调查了多少名购买者？
（2）请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为 度．
（3）若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
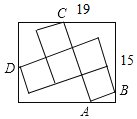
【题目】长和宽分别是19和15矩形内，如图所示放置5个大小相同的正方形，且A、B、C、D四个顶点分别在矩形的四条边上，则每个小正方形的边长是（ ）
A.
B.5.5C.
D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
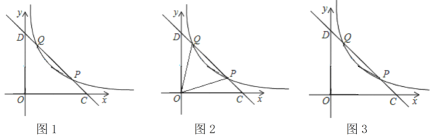
【题目】如图1，在平面直角坐标系xOy中，函数
（m为常数，m＞1，x＞0）的图象经过点P（m，1）和Q（1，m），直线PQ与x轴，y轴分别交于C，D两点.
（1）求∠OCD的度数；
（2）如图2，连接OQ、OP，当∠DOQ=∠OCD-∠POC时，求此时m的值；
（3）如图3，点A，点B分别在x轴和y轴正半轴上的动点.再以OA、OB为邻边作矩形OAMB.若点M恰好在函数（m为常数，m＞1，x＞0）的图象上，且四边形BAPQ为平行四边形，求此时OA、OB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
