
【题目】定义:二元一次不等式是指含有两个未知数(即二元),并且未知数的次数是1次(即一次)的不等式;满足二元一次不等式(组)的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式(组)的解集.如:x+y>3是二元一次不等式,(1,4)是该不等式的解.有序实数对可以看成直角坐标平面内点的坐标.于是二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合.
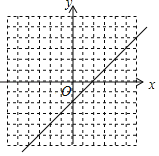
(1)已知A(![]() ,1),B (1,﹣1),C (2,﹣1),D(﹣1,﹣1)四个点,请在直角坐标系中标出这四个点,这四个点中是x﹣y﹣2≤0的解的点是 .
,1),B (1,﹣1),C (2,﹣1),D(﹣1,﹣1)四个点,请在直角坐标系中标出这四个点,这四个点中是x﹣y﹣2≤0的解的点是 .
(2)设 的解集在坐标系内所对应的点形成的图形为G.
的解集在坐标系内所对应的点形成的图形为G.
①求G的面积;
②P(x,y)为G内(含边界)的一点,求3x+2y的取值范围;
(3)设![]() 的解集围成的图形为M,直接写出抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围.
的解集围成的图形为M,直接写出抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围.
【答案】(1):A、B、D;(2)①3;②﹣12≤3x+2y≤1;(3)0≤m≤![]() .
.
【解析】
(1)在直角坐标系描出A、B、C、D四点,观察图形即可得出结论
(2)①分别画出直线y=2x+1、y=-x-2、y=-3得出图形为G,从而求出G的面积;
②根据P(x,y)为G内(含边界)的一点,求出x、y的范围,从而3x+2y的取值范围;
(3)分别画出直线y=2x+1、y=2x-1、y=-2x-1、y=-2x+1所围成的图形M,再根据抛物线的对称轴x=﹣m,和抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点,从而求出m的取值范围
解:(1)如图所示:
这四个点中是x﹣y﹣2≤0的解的点是A、B、D.
故答案为:A、B、D;
(2)①如图所示:
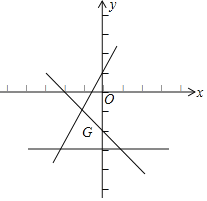
不等式组在坐标系内形成的图形为G,
所以G的面积为:![]() ×3×2=3.
×3×2=3.
②根据图象得:
﹣2≤x≤1,﹣3≤y≤﹣1,
∴﹣6≤3x≤3,﹣6≤2y≤﹣2,
∴﹣12≤3x+2y≤1.
答:3x+2y的取值范围为﹣12≤3x+2y≤1.
(3)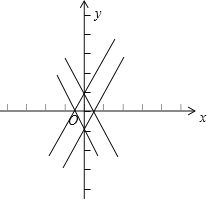
如图所示为
不等式组![]() 的解集围成的图形,设为M,
的解集围成的图形,设为M,
抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围:
∵抛物线的对称轴x=﹣m,
﹣m≥﹣![]() ,或﹣m≤
,或﹣m≤![]() ,
,
∴m![]() 或m≥﹣
或m≥﹣![]() .
.
又﹣1≤3m2﹣m﹣1≤1,
∴0≤m≤![]() ,
,
综上:m的取值范围是0≤m≤![]()


科目:初中数学 来源: 题型:
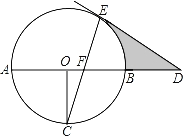
【题目】如图,在⊙O中,AB为⊙O的直径,过O点作OC⊥AB且交⊙O于C点,延长AB到D,过点D作⊙O的切线DE,切点为E,连接CE交AB于F点.
(1)求证:DE=DF;
(2)若⊙O的半径为2,求CF·CE的值;
(3)若⊙O的半径为2,∠D=30°,则阴影部分的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
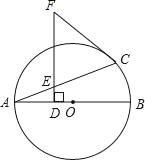
【题目】如图,AB是⊙O的直径,F是⊙O外一点,过点F作FD⊥AB于点D,交弦AC于点E,且FC=FE.
(1)求证:FC是⊙O的切线;
(2)若⊙O的半径为5,cos∠FCE=![]() ,求弦AC的长.
,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
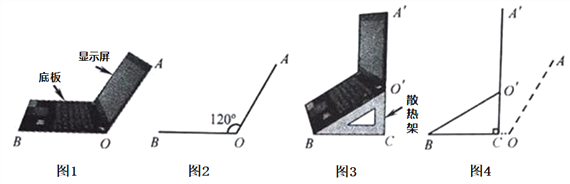
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是斜边AB上的中线,以
是斜边AB上的中线,以![]() 为直径的
为直径的![]() 分别交于
分别交于![]() 点
点![]() ,过点N作
,过点N作![]() ,垂足为
,垂足为![]() .
.
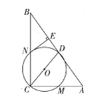
(1)求证:![]() 与
与![]() 相切;
相切;
(2)若![]() 半径为
半径为![]() ,
,![]() ,则
,则![]() 的长为_______________;
的长为_______________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
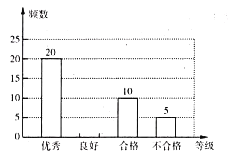
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“星光隧道”是贯穿新牌坊商圈和照母山以北的高端居住区的重要纽带,预计2017年底竣工通车,图中线段AB表示该工程的部分隧道,无人勘测飞机从隧道一侧的点A出发,沿着坡度为1:2的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为12°,继续飞行到点E,测得点B的俯角为45°,此时点E离地面高度EF=700米,则隧道BC段的长度约为( )米.(参考数据:tan12°≈0.2,cos12°≈0.98)
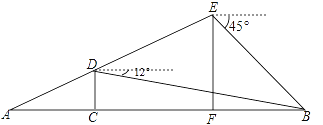
A. 2100 B. 1600 C. 1500 D. 1540
查看答案和解析>>
科目:初中数学 来源: 题型:
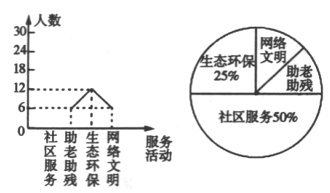
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
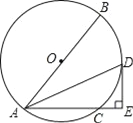
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com