练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

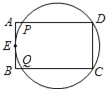
    【题目】如图的矩形ABCD中，E为AB的中点，有一圆过C、D、E三点，且此圆分别与AD、BC相交于P、Q两点．甲、乙两人想找到此圆的圆心O，其作法如下：

    (甲) 作∠DEC的角平分线L，作DE的中垂线，交L于O点，则O即为所求；

    (乙) 连接PC、QD，两线段交于一点O，则O即为所求.

    对于甲、乙两人的作法，下列判断何者正确？(　　)

    A. 两人皆正确 B. 两人皆错误

    C. 甲正确，乙错误 D. 甲错误，乙正确

    【答案】A

    【解析】

    根据线段垂直平分线的性质判断甲，根据90°的圆周角所对的弦是直径判断乙．

    解：甲，∵ED＝EC，
    ∴△DEC为等腰三角形，
    ∴L为CD之中垂线，
    ∴O为两中垂线之交点，
    即O为△CDE的外心，
    ∴O为此圆圆心．
    乙，∵∠ADC＝90°，∠DCB＝90°，
    ∴PC、QD为此圆直径，
    ∴PC与QD的交点O为此圆圆心，因此甲、乙两人皆正确．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

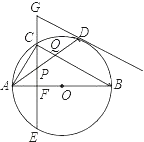
    【题目】如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心；④APAD＝CQCB．其中正确的是_____（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据：≈1.414，≈1.732）

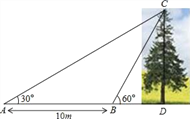
    【答案】8.7米

    【解析】试题分析：首先利用三角形的外角的性质求得∠ACB的度数，得到BC的长度，然后在直角△BDC中，利用三角函数即可求解．

    试题解析：∵∠CBD=∠A+∠ACB，

    ∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°，

    ∴∠A=∠ACB，

    ∴BC=AB=10（米）．

    在直角△BCD中，CD=BCsin∠CBD=10×=5≈5×1.732=8.7（米）．

    答：这棵树CD的高度为8.7米．

    考点：解直角三角形的应用

    【题型】解答题
    【结束】
    23

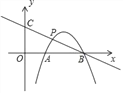
    【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+ax+b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C．

    （1）求抛物线y=﹣x2+ax+b的解析式；

    （2）当点P是线段BC的中点时，求点P的坐标；

    （3）在（2）的条件下，求sin∠OCB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

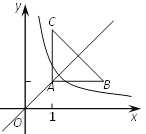
    【题目】如图，Rt△ABC在第一象限， ，AB=AC=2，点A在直线上，其中点A的横坐标为1，且AB∥轴，AC∥轴，若双曲线与有交点，则k的取值范围是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

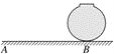
    【题目】如图是置于水平地面上的一个球形储油罐，小敏想测量它的半径、在阳光下，他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(如示意图，AB＝10米)；同一时刻，他又测得竖直立在地面上长为1米的竹竿的影子长为2米，那么，球的半径是________米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠B=90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM=2∠A．

    （1）判断直线MN与⊙O的位置关系，并说明理由；

    （2）若OA=4，∠BCM=60°，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

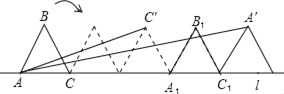
    【题目】如图，已知边长为2的正三角形ABC沿着直线l滚动．

    (1)当△ABC滚动一周到△A1B1C1的位置，此时A点运动的路程为　 　；约为　　；(精确到0.1，π＝3.14…)

    (2)设△ABC滚动240°时，C点的位置为C′，△ABC滚动480°时，A点的位置为A′．请你利用三角函数中正切的两角和公式tan(α+β)＝(tanα+tanβ)÷(1﹣tanαtanβ)，求出∠CAC′+∠CAA′的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”。

    （1）请写出两个为“同簇二次函数”的函数；

    （2）已知关于x的二次函数y1=2x2—4mx+2m2+1，和y2=ax2+bx+5，其中y1的图象经过点A（1，1），若y1+y2为y1为“同簇二次函数”，求函数y2的表达式，并求当0≤x≤3时，y2的最大值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，一次函数（为常数，）的图像与轴、轴分别相交于点，半径为4的⊙与轴正半轴相交于点，与轴相交于点，点在点上方.

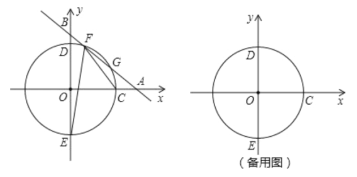
    （1）若直线与弧有两个交点.

    ①求的度数；

    ②用含的代数式表示，并直接写出的取值范围；

    （2）设，在线段上是否存在点，使？若存在，请求出点坐标；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案