
【题目】如图,在等边三角形ABC的三边上,分别取点D、E、F,使AD=BE=CF,
(1)求证:△DEF是等边三角形.
(2)若2BE=EC,求∠FEC的度数.
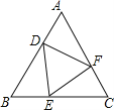
【答案】(1)见解析;(2)∠FEC=30°
【解析】
(1)由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.
(2)取EC的中点H,连接FH.只要证明FH=CH=EH,可得∠EFC=90°.
(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵AD=BE=CF,
∴AF=BD,
在△ADF和△BED中,
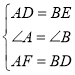 ,
,
∴△ADF≌△BED(SAS),
∴DF=DE,
同理DE=EF,
∴DE=DF=EF.
∴△DEF是等边三角形.
(2)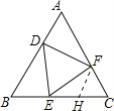
解:取EC的中点H,连接FH.
∵EC=2BE,EH=CH,BE=CF,
∴CH=CF,
∵∠C=60°,
∴△CFH都是等边三角形,
∴FH=CH=EH,
∴∠EFC=90°
∴∠FEC=30°


科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.
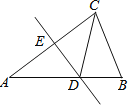
(1)若AB=10,BC=6,求△BCD的周长;
(2)若AD=BC,试求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解一批灯泡的使用寿命应采用普查的方式
B. 为了解一批共10000件产品的质量,从中抽取了2件进行检查均合格,估计该批产品的合格率为100%
C. 某有奖购物活动中奖率1%,则参与100次一定会有一次中奖
D. 甲乙两人在5次测试中平均分相同,![]() =2,
=2,![]() =0.8,则乙的成绩较为稳定
=0.8,则乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有长度分别为3cm、4cm、5cm、8cm的4根木条
(1)李鑫同学从中任取一根,抽到“长度是4cm的木条”的概率是 .
(2)在李鑫同学取出4cm的木条后,王华同学又从剩下的木条中,同时随机取出两根,求他们取出的三根木条能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小丽设计了A、B两种游戏:游戏A的规则是:用3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.游戏B的规则是:用4张数字分别是5、6、8、8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌,若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜,否则小丽获胜.请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
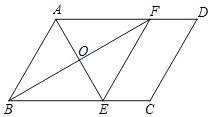
(1)求证:四边形ABEF是菱形;
(2)若AE=12,BF=16,CE=5,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com