
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.

【答案】(1)见解析 (2)见解析 (3)BD=DE-CE
【解析】
此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,利用了转化及等量代换的思想,熟练掌握全等三角形的判定与性质是解本题的关键.
(1)由BD垂直于AE,得到三角形ABD为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由∠BAC=90°,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,AB=AC,利用AAS可得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=AD+DE,等量代换即可得证;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系为BD=DE-CE,理由为:同(1)得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=DE-AD等量代换即可得证;
(3)由(1)(2)总结得到当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
解:(1)证明:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,
∵∠BAC=90°,∴∠BAD+∠EAC=90°∴∠ABD=∠EAC,
在△ABD和△CAE中
∵
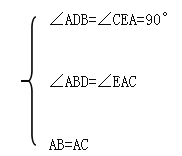
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD、DE、CE的关系为BD=DE-CE,理由为:
证明:在△ABD和△CAE中
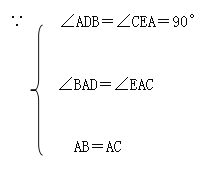
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE,
∵AE=DE-AD,
∴BD=DE-CE;
(3)当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.


科目:初中数学 来源: 题型:
【题目】为活跃校园气氛,增强班集体凝聚力,培养学生团结协作的意识,我校计划在初一、初二举行学生趣味运动会.学校计划用不超过4620元购买足球和篮球共28个,分别作为运动会团体一、二等奖的奖品.已知足球单价180元,篮球单价160元.
(1)学校至多可购买多少个足球?
(2)为了鼓励更多班级参与运动,学校决定在计划经费内,按(1)问的结果购买足球作为一等奖奖品.购买奖品时正好赶上商场对商品价格进行调整,足球单价上涨了a%,篮球单价下降了![]() a%,最终恰好比计划经费的最大值节余了196元,求a的值.
a%,最终恰好比计划经费的最大值节余了196元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由不同生产商提供![]() 套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的
套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的![]() 套校服.如果将其中只有
套校服.如果将其中只有![]() 人选中的校服称作“不受欢迎校服”,
人选中的校服称作“不受欢迎校服”,![]() 人选中的校服称作“颇受欢迎校服”,
人选中的校服称作“颇受欢迎校服”,![]() 人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
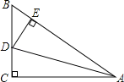
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论.①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
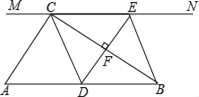
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
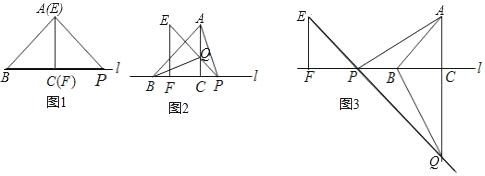
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com