
 如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→B→C→M路径匀速慢跑,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )
如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→B→C→M路径匀速慢跑,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 设⊙M的半径为r,李老师跑步的速度为v,分类讨论:当李老师在M→A时,y=vx;当李老师在A→B时,y不变,即y=r;当李老师在C→M时,y=r-vx,所以y与x的函数图象为三条线段,第1段和第3段的时间相等,第2段所用时间用其它两段的时间要多,由此特征可对四个选项进行判断.
解答 解:设⊙M的半径为r,李老师跑步的速度为v,
当0≤x≤$\frac{r}{v}$时,y=xv;
当$\frac{r}{v}$<x≤$\frac{(π+1)r}{v}$时,y=r,
当$\frac{(π+1)r}{v}$<x≤$\frac{(π+2)r}{v}$时,y=r-xv.
故选B.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是设⊙M的半径为r,李老师跑步的速度为v,利用分类讨论的思想求出y与x的函数关系式.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
| 日 期 | 28 | 29 | 30 | 1 | 2 | 3 |
| 水位记录 | +0.7 | +0.4 | -0.9 | -0.6 | +0.1 | -0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
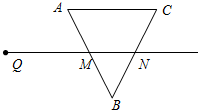 如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).
如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
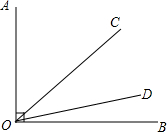 如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.
如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}=3$ | B. | $\sqrt{4}=±2$ | C. | $\sqrt{0.9}=0.3$ | D. | $\sqrt{{{({-2})}^2}}=-2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com