
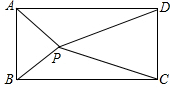
 如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.
如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2. 分析 过点P作AD的垂线,交AD于点E,交BC于点F;则四边形ABFE和CDEF为矩形,得出AE=BF,DE=CF,由勾股定理得出PA2,PC2,PB2,PD2,再比较PA2+PC2与PB2+PD2即可.
解答 证明:过点P作AD的垂线,交AD于点E,交BC于点F,如图所示:
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
点评 本题考查了矩形的性质与判定、勾股定理的运用;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | “任意四边形内角和为360°”是不可能事件 | |
| B. | “湘潭市明天会下雨”是必然事件 | |
| C. | “预计本题的正确率是95%”表示100位考生中一定有95人做对 | |
| D. | 抛掷一枚质地均匀的硬币,正面朝上的概率是$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | m=8n | B. | m=8+6n | C. | m=4+4n | D. | m=2+6n |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
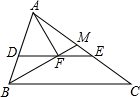 如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.
如图,已知△ABC中,∠ABC的平分线为BM,过A作AF⊥BM,垂足为F,过F作BC的平行线交AB于D,交AC于E,EF=2,AB=6,则BC=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<1 | B. | k<-1 | C. | k>-1 | D. | k>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com