
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.
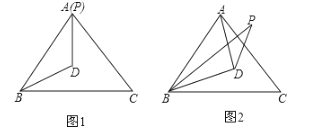
(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
【答案】(1)30°;(2)30°;(3)∠BPD=30°或150°.
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠DPB,因为DB是∠PBC的平分线,因此,∠DBP=∠DPB=30°;
(2)连接CD,BP=BC,BD又是∠PBC的平分线,则△PBD≌△CBD,有∠BPD=∠BCD,那么关键是求∠BCD的值,可通过证明△ACD和△BCD全等来得出,∠BCD=∠ACD=30°,然后求出∠BPD的度数;
(3)同(2)的证法完全一样,先求出∠BCD的度数,然后证明△BPD≌△BCD.(当∠BPD是钝角时,∠BPD=∠BCD=(360-60)÷2=150°,还是用的(2)中的△BPD≌△BCD,△BCD≌△ACD).
解:(1)在等边三角形ABC中,
∴∠ABC=∠PBC=60°,
∵DB平分∠PBC,
∴∠PBD=30°
∵DB=DA,
∴∠DBP=∠DPB=30°;
(2)如图,连接CD,
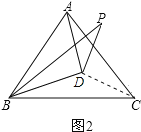
∵点D在∠PBC的平分线上
∴∠PBD=∠CBD
∵△ABC是等边三角形
∴BA=BC=AC,∠ACB=60°
∵BP=BA
∴BP=BC
∵BD=BD
∴△PBD≌△CBD(SAS)
∴∠BPD=∠BCD
∵DB=DA,BC=AC,CD=CD
∴△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°
∠ACB=30°
∴∠BPD=30°;
(3)当BP在∠ABC的外部时,如图
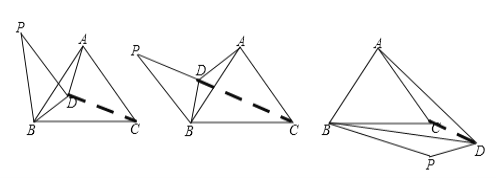
当∠BPD是锐角时,由(2)知,△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°,
∠ACB=30°,
由△PBD≌△CBD,
∴∠BPD=30°;
当∠BPD是钝角时,由(2)知,△BCD≌△ACD
∴∠BCD=∠ACD,
∴∠BCD=(360°-60°)÷2=150°,
由△PBD≌△CBD,
∴∠BPD=∠BCD=150°;
综合上述,∠BPD=30°或150°.


科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
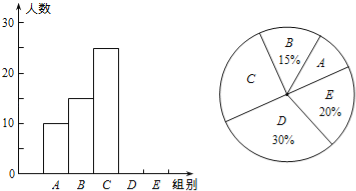
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
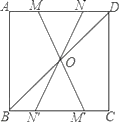
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
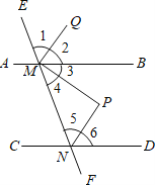
【题目】如图,AB∥CD,直线EF分别与AB,CD相交于M,N,∠AME=60°
(1)求∠DNF的度数;
(2)若∠P=90°,∠2=∠6=60°,求证:MP平分∠BMN.
查看答案和解析>>
科目:初中数学 来源: 题型:
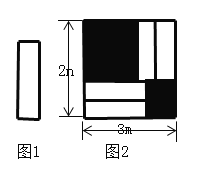
【题目】把四张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为![]() 厘米,宽为
厘米,宽为![]() 厘米))的盒了底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是____________厘米
厘米))的盒了底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是____________厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的 3 倍,则它们第 2018 次相遇在边( )上.
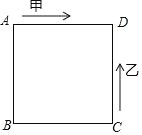
A. CDB. ADC. ABD. BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:![]() ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com