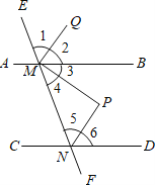
【题目】如图，AB∥CD，直线EF分别与AB，CD相交于M，N，∠AME=60°
（1）求∠DNF的度数；
（2）若∠P=90°，∠2=∠6=60°，求证：MP平分∠BMN．
【答案】（1）∠DNF =60°；（2）见解析
【解析】
(1)利用对顶角相等和两直线平行同位角相等可求；
(2)先利用邻补角互补及已知条件求出∠1=∠5=60°，最后借助平行线及角的和差求出∠3=∠4=30°，即可说明MP平分∠BMN．
解：(1)∵AB∥CD，∠AME=60°，
∴∠CNE=∠AME=60°．
∴∠DNF=∠CNE=60°．
(2)证明：∵∠AME+∠1+∠2=180°，∠DNF+∠5+∠6=180°，
∠2=∠6=60°，∠AME=60°，∠DNF=60°，
∴∠1=∠5=60°，
∴MQ∥NP，
∴∠PMQ=∠P=90°．
∴∠3=∠PMQ-∠2=30°．
∵∠1+∠2+∠3+∠4=∠EMN=180°，
∴∠4=180°-∠1-∠2-∠3=30°．
∴∠3=∠4，
∴MP平分∠BMN．
科目：初中数学 来源： 题型：
【题目】如图，将含有30°角的直角三角板ABC放入平面直角坐标系，顶点A，B分别落在x、y轴的正半轴上，∠OAB＝60°，点A的坐标为（1，0），将三角板ABC沿x轴向右作无滑动的滚动（先绕点A按顺时针方向旋转60°，再绕点C按顺时针方向旋转90°，…）当点B第一次落在x轴上时，则点B运动的路径与坐标轴围成的图形面积是________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市居民使用自来水按如下标准收费（水费按月缴纳）
月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
（1）当
时，某用户用了
水，求该用户这个月应该缴纳的水费；
（2）设某用户用水量为
立方米，求该用户应缴纳的水费（用含
的式子表达）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题中是真命题的是（ ）
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 两条平行直线被第三条直线所截，则一组同旁内角的平分线互相垂直
C. 三角形的一个外角等于两个内角的和
D. 等边三角形既是中心对称图形，又是轴对称图形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点E是等边△ABC的边BC上一点，以AE为边作等边△AEF，EF交AC于D.
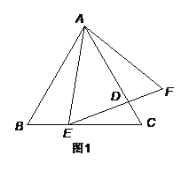
（1）连接CF，求证：
（2）如图2，作EH AF交AB于点H.
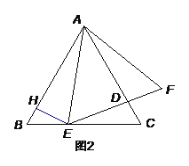
①求证：
；
②若EH=2，ED=4，直接写出BE的长为 _________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC是等边三角形，P为平面内的一个动点，BP=BA，0<∠PBC<180 ，DB平分∠PBC，且DB=DA．
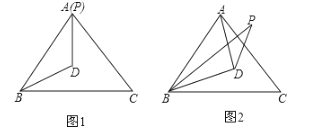
（1）当BP与BA重合时（如图1），求∠BPD的度数；
（2）当BP在∠ABC的内部时(如图2)，求∠BPD的度数；
（3）当BP在∠ABC的外部时，请你直接写出∠BPD的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某景区一电瓶小客车接到任务从景区大门出发，向东走2千米到达A景区，继续向东走2.5千米到达B景区，然后又回头向西走8.5千米到达C景区，最后回到景区大门．
（1）以景区大门为原点，向东为正方向，以1个单位长表示1千米，建立如图所示的数轴，请在数轴上表示出上述A、B、C三个景区的位置．
（2）若电瓶车充足一次电能行走15千米，则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务？请计算说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
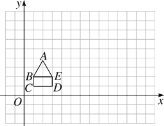
【题目】已知：如图，是由一个等边△ABE和一个矩形BCDE拼成的一个图形，其点B，C，D的坐标分别为(1，2)，(1，1)，(3，1)．
(1)直接写出E点和A点的坐标；
(2)试以点B为位似中心，作出位似图形A1B1C1D1E1，使所作的图形与原图形的位似比为3∶1；
(3)直接写出图形A1B1C1D1E1的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知□ABCD中，A（1，3）, B（2，-1）, C（5，-5）
（1）D的坐标为____________.
（2）若经过原点的一条直线平分□ABCD的面积，求此直线的解析式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
