
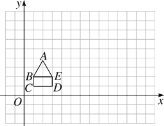
【题目】已知:如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其点B,C,D的坐标分别为(1,2),(1,1),(3,1).
(1)直接写出E点和A点的坐标;
(2)试以点B为位似中心,作出位似图形A1B1C1D1E1,使所作的图形与原图形的位似比为3∶1;
(3)直接写出图形A1B1C1D1E1的面积.
【答案】(1) E(3,2),A(2,2+![]() );(2)见解析;(3)18+9
);(2)见解析;(3)18+9![]() .
.
【解析】(1)由平面直角坐标系与网格,得出E的坐标,由等边三角形ABE的边长为2,求出BE边上的高,确定出A的纵坐标,而A的横坐标为2,即可求出A的坐标;
(2)连接BA并延长,使BA1=3BA,连接BE并延长,使BE1=3BE,连接BD并延长,使BD1=3BD,连接BC并延长,使BC1=3BC,连接A1E1,E1D1,D1C1,C1B,五边形A1B1C1D1E1为所求作的图形;
(3)由五边形ABCDE与五边形A1B1C1D1E1相似,且相似比为1:3,得到面积之比为1:9,求出五边形ABCDE的面积,即可得出五边形A1B1C1D1E1的面积.
(1)由图形可得E(3,2),∵△ABE为边长为2的等边三角形,∴BE边长的高为![]() ,∴A(2,2+
,∴A(2,2+![]() );
);
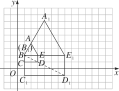
(2)如图所示,五边形A1B1C1D1E1为所求的图形;
(3)∵△ABE为边长是2的等边三角形,∴S△ABE=![]() ×22=
×22=![]() ,又矩形BCDE的面积为1×2=2,∴五边形ABCDE的面积为2+
,又矩形BCDE的面积为1×2=2,∴五边形ABCDE的面积为2+![]() .∵五边形ABCDE与五边形A1B1C1D1E1相似,且相似比为1∶3,则五边形A1B1C1D1E1的面积为9(2+
.∵五边形ABCDE与五边形A1B1C1D1E1相似,且相似比为1∶3,则五边形A1B1C1D1E1的面积为9(2+![]() )=18+9
)=18+9![]() .
.


科目:初中数学 来源: 题型:
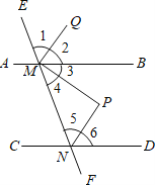
【题目】如图,AB∥CD,直线EF分别与AB,CD相交于M,N,∠AME=60°
(1)求∠DNF的度数;
(2)若∠P=90°,∠2=∠6=60°,求证:MP平分∠BMN.
查看答案和解析>>
科目:初中数学 来源: 题型:
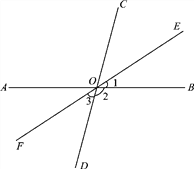
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的 3 倍,则它们第 2018 次相遇在边( )上.
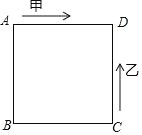
A. CDB. ADC. ABD. BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
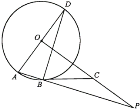
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
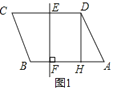
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
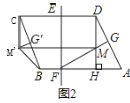
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
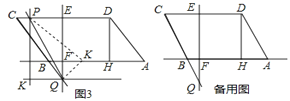
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com