
【题目】如图,点A,B,C在⊙O上,已知∠ABC=130°,则∠AOC=( )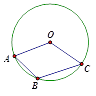
A.100°
B.110°
C.120°
D.130°
【答案】A
【解析】在优弧AC上取点D,连接AD,CD,
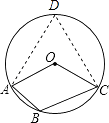
∵四边形ABCD是圆内接四边形,∠ABC=130°,
∴∠D=180°-130°=50°.
∵∠D与∠AOC是同弧所对的圆周角与圆心角,
∴∠AOC=2∠D=100°.
所以答案是:A.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对圆内接四边形的性质的理解,了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.


科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( ) 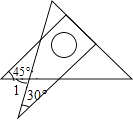
A.75°
B.65°
C.45°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (![]() a +b)(b -
a +b)(b -![]() a)
a)
C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E. 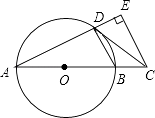
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式,黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,黄先生若乘汽车去福州,那么他此行与乘飞机相比减少二氧化碳排放量多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
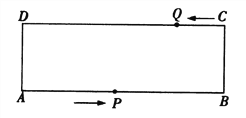
【题目】如图,在矩形ABCD中,AB=24 cm, BC=8 cm,点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从点C开始沿CD边以2 cm/s的速度移动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts.当t为何值时,四边形QPBC为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点![]() 的坐标分别是
的坐标分别是![]() 且
且![]() .
.

(1)求![]() 的值;
的值;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使三角形
,使三角形![]() 的面积是
的面积是![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)已知点![]() 是
是![]() 轴正半轴上一点,且到
轴正半轴上一点,且到![]() 轴的距离为
轴的距离为![]() ,若
,若![]() 点沿
点沿![]() 轴负半轴方向以每秒
轴负半轴方向以每秒![]() 个单位长度平移至点
个单位长度平移至点![]() ,当运动时间
,当运动时间![]() 为多少秒时,四边形
为多少秒时,四边形![]() 的面积
的面积![]() 为
为![]() 个平方单位?并写出此时点
个平方单位?并写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com