
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
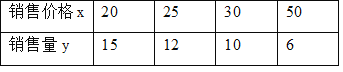
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式.
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
【答案】(1)画图见解析;(2)(2)![]() ;(3)当
;(3)当![]() 时,
时, ![]()
【解析】(1)根据描点法作函数的图象,先描点,连线即可得到答案,
(2)观察表中数据可得,x与y的积为常数,判断为反比例函数,根据数据,易得k的值,进而可得函数关系式,
(3)根据题意,易得关系式,根据反比例函数的单调性分析可得答案.
解:(1)根据描点法作函数的图象,先描点,连线即可得图象,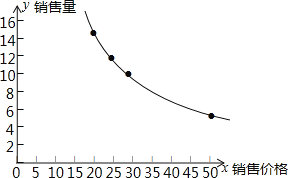
(2)观察表中数据可得,x与y得积为常数,判断为反比例函数,
根据数据,易得K=20×15=300,
故其解析式为y=![]() .
.
(3)w=(x-15) ![]() =300-
=300-![]() ;
;
当x≤30时,因为w随x增大而增大,
∴当x=30时,w最大=150.
“点睛”主要考查了函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.本题尤其要注意分两种情况考虑,然后根据数据的规律舍去一种情况.


科目:初中数学 来源: 题型:
【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的各边与坐标轴都平行,点A,C的坐标分别为(-1,1),(![]() ,-2
,-2![]() ).
).
(1)求点B,D的坐标.
(2)一动点P从点A出发,沿长方形的边AB,BC运动至点C停止,运动速度为每秒![]() 个单位长度,设运动时间为t s.
个单位长度,设运动时间为t s.
①当t=1时,求点P的坐标;
②当t=3时,求三角形PDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
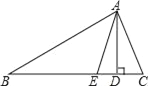
【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度数;
(2)写出∠DAE与∠ACB﹣∠ABC的数量关系: ,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
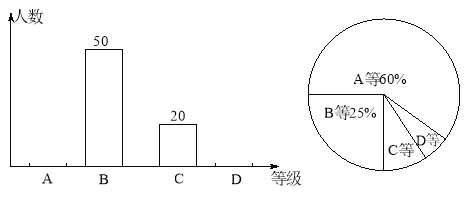
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%,根据统计图解答下列问题: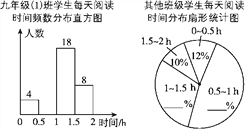
(1)九年级(1)班有________名学生.
(2)补全频数分布直方图.
(3)除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,请你补全扇形统计图.
(4)求该年级每天阅读时间不少于1 h的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
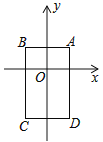
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com