
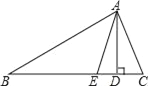
【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度数;
(2)写出∠DAE与∠ACB﹣∠ABC的数量关系: ,并证明你的结论.
【答案】(1)∠DAE=10°;(2)∠DAE=![]() (∠ACB﹣∠ABC),理由见解析.
(∠ACB﹣∠ABC),理由见解析.
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°﹣∠B﹣∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C﹣∠B的关系.
试题解析:(1)∵∠ABC=30°,∠ACB=50°,
∴∠CAB=180°﹣∠B﹣∠C=100°,
∵AE是△ABC角平分线,
∴∠CAE=![]() ∠CAB=50°,
∠CAB=50°,
∵AD分别是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=40°,
∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
(2)∠DAE=![]() (∠ACB﹣∠ABC),
(∠ACB﹣∠ABC),
理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,
∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=![]() (180°﹣∠B﹣∠C),
(180°﹣∠B﹣∠C),
∴∠DAE=![]() (180°﹣∠B﹣∠C)﹣(90°﹣∠C)=
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B).
(∠C﹣∠B).


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
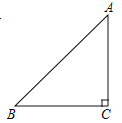
【题目】在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
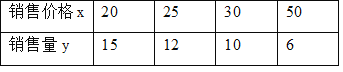
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式.
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,点F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连接FE,FC,BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.求证:△AGC∽△KGB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究应用:用“∪”、“∩”定义两种新运算:对于两数a、b,规定a∪b=10a×10b,a∩b=10a÷10b,例如:3∪2=103×102=105,3∩2=103÷102=10.
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值;
(3) 当x为何值时, (x∪5)的值与 (23∩17)的值相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com