
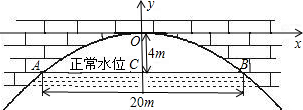
 有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.
有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.分析 (1)设该抛物线的解析式是y=ax2,结合图象,只需把(10,-4)代入求解;
(2)根据(1)中求得的函数解析式,把x=9代入求得y的值,从而可确定出水位上涨多少米时就会影响船只航行.
解答 解:(1)设该抛物线的解析式是y=ax2,
结合图象,把(10,-4)代入,得
100a=-4,
a=-$\frac{1}{25}$,则该抛物线的解析式是y=-$\frac{1}{25}$x2.
(2)当x=9时,则有y=-$\frac{1}{25}$×81=-3.24,
-3.24-(-4)=0.76(米).
答:水位上涨0.76米时,就会影响过往船只航行.
点评 此题考查了二次函数在实际问题中的应用,能够熟练运用待定系数法求得二次函数的解析式是解题的关键.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2 | B. | $\frac{1}{x-2}$ | C. | $\frac{{x}^{2}+4}{x-2}$ | D. | x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
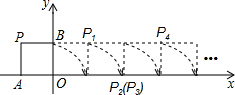 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com