
 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.分析 (1)根据平行线分线段成比例定理即可列方程求得;
(2)由QM∥AC,利用平行线分线段成比例定理可得$\frac{DQ}{DC}$=$\frac{DM}{AD}$,则MD即可利用t表示出来,然后利用S=S梯形MPCD-S△MDQ-S△PCQ写出函数解析式;
(3)根据S△PQM:S矩形ABCD=9:32,求得△PQM的面积,然后根据(2)即可列方程,解方程求解.
解答 解:(1)∵PQ∥BD,∴$\frac{CP}{BP}$=$\frac{CQ}{DQ}$,即$\frac{8-t}{t}$=$\frac{t}{6-t}$,解得:t=$\frac{24}{7}$;
(2)BP=t,PC=8-t,CQ=t,DQ=6-t,
∵QM∥AC,
∴$\frac{DQ}{DC}$=$\frac{DM}{AD}$,即$\frac{6-t}{t}$=$\frac{DM}{8}$,
∴DM=$\frac{4}{3}$(6-t),
∴S=S梯形MPCD-S△MDQ-S△PCQ=$\frac{1}{2}$×6×[$\frac{4}{3}$(6-t)+8-t)-$\frac{1}{2}$×$\frac{4}{3}$(6-t)2-$\frac{1}{2}$t(8-t)=-$\frac{1}{6}$t2-3t+24.
(3)∵S矩形ABCD=6×8=48,
又∵S△PQM:S矩形ABCD=9:32,
∴S△PQM=$\frac{27}{2}$.
∴-$\frac{1}{6}$t2-3t+24=$\frac{27}{2}$.
解得:t=3或-21(舍去).
点评 本题考查了平行线分线段成比例定理和矩形的性质,利用平行线分线段成比例定理利用t表示出DM,表示出S和t的关系是关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
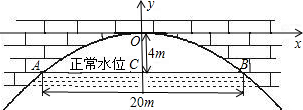 有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.
有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,∠CAB=∠BCA,CE⊥BD.
如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,∠CAB=∠BCA,CE⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)(x-1)=x2-x | B. | ${x^2}-\frac{1}{x}=0$ | C. | ax2+bx+c=0 | D. | x2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=5,BC=6,AC=7 | B. | AB=5,BC=6,∠B=45° | ||
| C. | AB=5,AC=4,∠C=90° | D. | AB=5,AC=4,∠C=45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com