
 直线y=
直线y=| 2 |
| 3 |
| k |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| k |
| x |
| 12 |
| x |
| 3 |
| 2 |
| 4 |
| 9 |
| 2 |
| 3 |
| 9 |
| 2 |
| 2 |
| 9 |


科目:初中数学 来源: 题型:
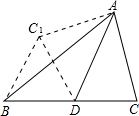 如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( )
如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( )| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、向左平移1个单位,再向下平移3个单位 |
| B、向左平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向右平移1个单位,再向上平移3个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 “汶川”地震后,成都乙粮库以每天相同的速度将粮食运往灾区,为缓解成都乙粮库的压力,河南省甲粮库以汽车运输的方式予以支援,如图是两粮库的储粮量y(万吨)与时间x(天)之间的函数图象,在单位时间内甲粮库的出粮量与乙粮库的进粮量是相同的(不考虑粮食的损耗),通过图象回答下列问题.
“汶川”地震后,成都乙粮库以每天相同的速度将粮食运往灾区,为缓解成都乙粮库的压力,河南省甲粮库以汽车运输的方式予以支援,如图是两粮库的储粮量y(万吨)与时间x(天)之间的函数图象,在单位时间内甲粮库的出粮量与乙粮库的进粮量是相同的(不考虑粮食的损耗),通过图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com