
ЗжЮі ЃЈ1ЃЉжЛашАбЕуAЁЂCЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНОЭПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩЬтПЩЕУ|yQ|=|yC|=6ЃЌДгЖјЕУЕНyQ=ЁР6ЃЌДњШыХзЮяЯпЕФНтЮіЪНЃЌОЭПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉгЩгкBDЪЧЖЈжЕЃЌвЊЪЙЁїBDMЕФжмГЄзюаЁЃЌжЛашMB+MDзюаЁЃЌзїЕуBЙигкжБЯпACЕФЖдГЦЕуЮЊBЁфЃЌСЌНсBBЁфНЛACгкFЃЌСЌНсBЁфDЃЌBЁфDгыACЕФНЛЕуОЭЪЧвЊЬНЧѓЕФЕуMЃЎзїBЁфEЁЭxжсгкEЃЌШчЭМЫљЪОЃЌвЊЧѓЕуMЕФзјБъЃЌжЛашЧѓГіжБЯпBЁфDгыжБЯпACЕФНтЮіЪНЃЌжЛашЧѓГіЕуBЁфЕФзјБъЃЌПЩЭЈЙ§ЁїBAFЁзЁїCAOЧѓГіBFЃЌДгЖјЧѓГіBBЁфЃЌдйЭЈЙ§ЁїBBЁфEЁзЁїBAFЧѓГіBEЃЌНјЖјПЩЧѓГіOEЁЂBЁфEЃЌЮЪЬтЕУвдНтОіЃЎ
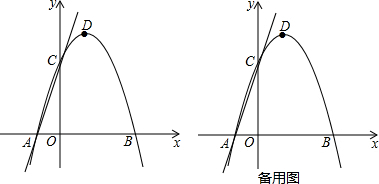
НтД№ НтЃКЃЈ1ЃЉЁпAЃЈ-2ЃЌ0ЃЉЃЌ CЃЈ0ЃЌ6ЃЉдкХзЮяЯпy=-x2+ax+bЩЯЃЌ
Ёр$\left\{\begin{array}{l}{-4-2a+b=0}\\{b=6}\end{array}\right.$ЃЌ
НтЕУЃК$\left\{\begin{array}{l}{a=1}\\{b=6}\end{array}\right.$ЃЌ
ЁрaЁЂbЕФжЕЗжБ№ЮЊ1ЁЂ6ЃЛ
ЃЈ2ЃЉЂйШєЕуQдкxжсЕФЩЯЗНЃЌдђyQ=yC=6ЃЌ
Ёр-x2+x+6=6ЃЌ
НтЕУx1=0ЃЌx2=1ЃЌ
ЁрQЃЈ1ЃЌ6ЃЉЃЛ
ЂкШєЕуQдкxжсЕФЯТЗНЃЌдђyQ=-yC=-6ЃЌ
Ёр-x2+x+6=-6ЃЌ
НтЕУx1=4ЃЌx2=-3ЃЌ
ЁрQЃЈ4ЃЌ-6ЃЉЛђЃЈ-3ЃЌ-6ЃЉЃЎ
злЩЯЫљЪіЃКЗћКЯЬѕМўЕФЕуQЕФзјБъЮЊЃЈ1ЃЌ6ЃЉЁЂЃЈ4ЃЌ-6ЃЉЁЂЃЈ-3ЃЌ-6ЃЉЃЛ
ЃЈ3ЃЉЩшЕуBЙигкжБЯпACЕФЖдГЦЕуЮЊBЁфЃЌСЌНсBBЁфНЛACгкFЃЌ
СЌНсBЁфDЃЌBЁфDгыACЕФНЛЕуОЭЪЧвЊЬНЧѓЕФЕуMЃЎ
зїBЁфEЁЭxжсгкEЃЌШчЭМЫљЪОЃЌ
ЁпAO=2ЃЌCO=6ЃЌ
ЁрAC=2$\sqrt{10}$ЃЎ
Сюy=0ЃЌЕУ-x2+x+6=0ЃЌ
НтЕУx1=3ЃЌx2=-2ЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌAB=3-ЃЈ-2ЃЉ=5ЃЎ
гЩy=-x2+x+6=-ЃЈx-$\frac{1}{2}$ЃЉ2+$\frac{25}{4}$ПЩЕУЃЌ
ЖЅЕуDЕФзјБъЃЈ$\frac{1}{2}$ЃЌ$\frac{25}{4}$ЃЉЃЎ
ЁпЁЯCAO=ЁЯBAFЃЌЁЯAOC=ЁЯAFB=90ЁуЃЌ
ЁрЁїBAFЁзЁїCAOЃЌ
Ёр$\frac{BF}{CO}$=$\frac{AB}{AC}$ЃЌ
Ёр$\frac{BF}{6}$=$\frac{5}{2\sqrt{10}}$ЃЌ
ЁрBF=$\frac{3\sqrt{10}}{2}$ЃЌ
ЁрBBЁф=3$\sqrt{10}$ЃЎ
ЁпЁЯABF=ЁЯBЁфBEЃЌЁЯBЁфEB=ЁЯAFB=90ЁуЃЌ
ЁрЁїBBЁфEЁзЁїBAFЃЌ
Ёр$\frac{BE}{BF}$=$\frac{BBЁф}{BA}$ЃЌ
Ёр$\frac{BE}{\frac{3\sqrt{10}}{2}}$=$\frac{3\sqrt{10}}{5}$ЃЌ
ЁрBE=9ЃЌ
ЁрOE=9-3=6ЃЌBЁфE=$\sqrt{BB{Ёф}^{2}-B{E}^{2}}$=3ЃЌ
ЁрBЁфЃЈ-6ЃЌ3ЃЉЃЎ
ЩшжБЯпACЕФНтЮіЪНЮЊy=mx+nЃЌ
дђга$\left\{\begin{array}{l}{-2m+n=0}\\{n=6}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{m=3}\\{n=6}\end{array}\right.$ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=3x+6ЃЎ
ЭЌРэжБЯпBЁфDЕФНтЮіЪНЮЊy=$\frac{1}{2}$x+6ЃЌ
Нт$\left\{\begin{array}{l}{y=3x+6}\\{y=\frac{1}{2}x+6}\end{array}\right.$ЃЌЕУ
$\left\{\begin{array}{l}{x=0}\\{y=6}\end{array}\right.$ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЎ
ЕуЦР БОЬтжївЊПМВщСЫХзЮяЯпЩЯЕуЕФзјБъЬиеїЁЂдЫгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯпМАХзЮяЯпЕФНтЮіЪНЁЂЧѓСНжБЯпЕФНЛЕузјБъЁЂСНЕужЎМфЯпЖЮзюЖЬЁЂЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЁЂЦНааЫФБпаЮЕФаджЪЁЂНтвЛдЊЖўДЮЗНГЬЁЂЙДЙЩЖЈРэЕШжЊЪЖЃЌгЩЬѕМўЕУЕН|yQ|=|yC|=6ЪЧНтОіЕкЃЈ2ЃЉаЁЬтЕФЙиМќЃЌдЫгУжсЖдГЦадМАСНЕужЎМфЯпЖЮзюЖЬЪЧНтОіЕкЃЈ3ЃЉаЁЬтЕФЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
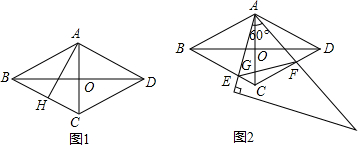
 ШчЭМЃЌАбвЛИіГЄЗНаЮжНЬѕABCDбиEFелЕўЃЌШєЁЯ1=55ЁуЃЌдђЁЯAEG=70ЃЎ
ШчЭМЃЌАбвЛИіГЄЗНаЮжНЬѕABCDбиEFелЕўЃЌШєЁЯ1=55ЁуЃЌдђЁЯAEG=70ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 0КЭ1жЎМф | BЃЎ | 1КЭ2жЎМф | CЃЎ | 2КЭ3жЎМф | DЃЎ | 3КЭ4жЎМф |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com