
【题目】如图,在平面直角坐标系中,点O为坐标原点,平移抛物线y=x2﹣2x+3,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,求平移后的抛物线的解析式.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
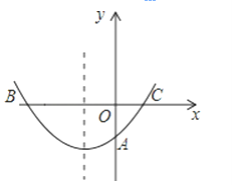
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,交y轴于点A.
(1)根据图象确定a,b,c的符号;
(2)如果OC=OA=![]() OB,BC=4,求这个二次函数的解析式.
OB,BC=4,求这个二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
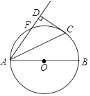
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
=![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
A. 2 ![]() B. 4
B. 4 ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
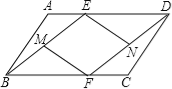
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为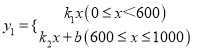 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
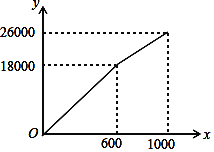
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD下方一点,将△PCD绕点P顺时针旋转60°后,恰好点D与点A重合,得到△PEA,连接EB,问:△ABE是什么特殊三角形?请说明理由.
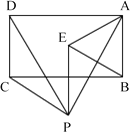
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com