
【题目】如图,在![]() ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=
ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=![]() .
.
(1)求证:四边形ABDE是平行四边形;
(2)求AB的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据两组对边分别平行的四边形是平行四边形即可得到结论;
(2)由(1)知,AB=DE=CD,即D是CE的中点,在直角△CEF中利用30°所对的直角三角形的性质以及勾股定理即可求得到CE的长,进而可求出AB的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥DE.
∵AE∥BD,
∴四边形ABDE是平行四边形.
(2)解:∵EF⊥BC,∴∠EFC=90°.
∵AB∥EC,∴∠ECF=∠ABC=60°.
∴∠CEF=30°.
∵CF=![]() ,
,
∴CE=2CF=2![]() .
.
∵四边形ABCD和四边形ABDE都是平行四边形,
∴AB=CD=DE,∴CE=2AB,
∴AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F.

(1)求证:GE=GF;
(2)填空:若BD=1,则DF的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长方形的长和宽分别为x厘米和y厘米(x,y为正整数),如果将长方形的长和宽各增加5厘米得到新的长方形,面积记为![]() ,将长方形的长和宽各减少2厘米得到新的长方形,面积记为
,将长方形的长和宽各减少2厘米得到新的长方形,面积记为![]() .
.
(1)请说明:![]() 与
与![]() 的差一定是7的倍数.
的差一定是7的倍数.
(2)如果![]() 比
比![]() 大196
大196![]() ,求原长方形的周长.
,求原长方形的周长.
(3)如果一个面积为![]() 的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由.
的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 和点
和点![]() 关于原点对称,点
关于原点对称,点![]() 是直线
是直线![]() 位于
位于![]() 轴右侧部分图象上一点,连接
轴右侧部分图象上一点,连接![]() ,已知
,已知![]() .
.
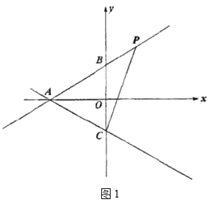
(1)求直线![]() 的解析式;
的解析式;
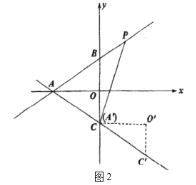
(2)如图2,![]() 沿着直线
沿着直线![]() 平移得
平移得![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合.点
重合.点![]() 为直线
为直线![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出
的值最小时,请求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
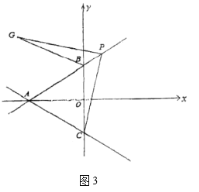
(3)如图3,将![]() 沿直线
沿直线![]() 是翻折得
是翻折得![]() 点
点![]() 为平面内任意一动点,在直线
为平面内任意一动点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形是矩形;若存在,请直接写出点
为顶点的四边形是矩形;若存在,请直接写出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:设a+b
)2,善于思考的小明进行了以下探索:设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为正整数),则有a+b
)2(其中a,b,m,n均为正整数),则有a+b![]() =m2+2n2+2
=m2+2n2+2![]() mn,∴a=m2+2n2,b=2mn.
mn,∴a=m2+2n2,b=2mn.
这样小明就找到了一种把a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= ;
)2,用含m,n的式子分别表示a,b,得a= ,b= ;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:4+2 =(1+ )2;(答案不唯一)
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)探究1:连接对角线AC,BD由三角形中位线定理及平行四边形的判定定理易得四边形EFGH为 (不需要证明);
(2)探究2:观察猜想:
①当四边形ABCD的对角线AC,BD满足条件 时,四边形EFGH是菱形;
②当四边形ABCD的对角线AC,BD满足条件 时,四边形EFGH为矩形.
(3)探究3:当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A.5
B.![]()
C.5 ![]()
D.5 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,…和C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2020的纵坐标是_____,点Bn的纵坐标是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com