
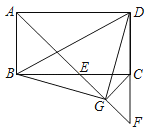
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG.
(1)求证:△DCG≌△BEG;
(2)你能求出∠BDG的度数吗?若能,请写出计算过程;若不能,请说明理由.
【答案】(1)见解析;(2)∠BDG=45°,计算过程见解析
【解析】
(1)先求出∠BAE=45°,判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AB=BE,∠AEB=45°,从而得到BE=CD,再求出△CEF是等腰直角三角形,根据等腰直角三角形的性质可得CG=EG,再求出∠BEG=∠DCG=135°,然后利用“边角边”证明即可.
(2)由△DCG≌△AEG,得出∠DGC=∠BGE,证出∠BGD=∠EGC=90°,即可得出结果.
(1)证明:∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
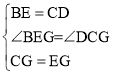 ,
,
∴△DCG≌△BEG(SAS).
(2)解:∵△DCG≌△BEG,
∴∠DGC=∠BGE,DG=BG,
∴∠BGD=∠EGC=90°,
∴△BDG等腰直角三角形,
∴∠BDG=45°.


科目:初中数学 来源: 题型:
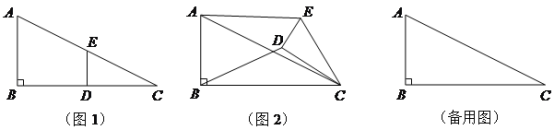
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
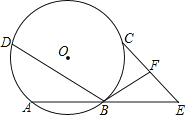
【题目】如图,A、B、C,D在⊙O上,且![]() =
=![]() ,E是AB延长线上一点,且BE=AB,F是CE中点,
,E是AB延长线上一点,且BE=AB,F是CE中点,![]() 为80°
为80°
(1)求证:BD=2BF;
(2)试探究:当∠E等于多少度时,BD∥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一块直角三角形ABC,∠B=90°,AB=3,BC=4,截得两个正方形DEFG,BHJN,设S1=DEFG的面积,S2=BHJN的面积,则S1、S2的大小关系是( )
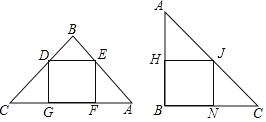
A.S1>S2B.S1<S2C.S1=S2D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
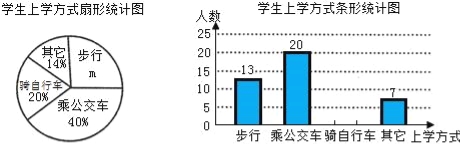
(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳参加图书馆标志设计大赛,他在边长为2的正方形ABCD内作等边△BCE,并与正方形的对角线交于F、G点,制成了图中阴影部分的标志,则这个标志AFEGD的面积是_____.
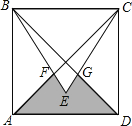
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
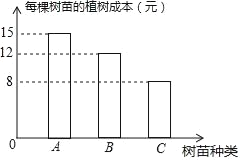
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com