
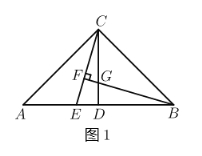
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点,直线
边上一点,直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)如图2,直线![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG;
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠BCD=45°,∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG.
又∵BF⊥CE,∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG.
在△AEC和△CGB中,∵ ,∴△AEC≌△CGB(ASA),∴AE=CG;
,∴△AEC≌△CGB(ASA),∴AE=CG;
(2)∵CH⊥HM,CD⊥ED,∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC.
在△BCE和△CAM中,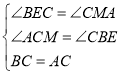 ,∴△BCE≌△CAM(AAS),∴BE=CM.
,∴△BCE≌△CAM(AAS),∴BE=CM.


科目:初中数学 来源: 题型:
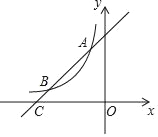
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
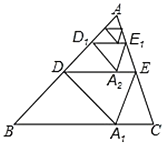
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,折痕
处,称为第1次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,折痕
处,称为第2次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,按上述方法不断操作下去…经过第2020次操作后得到的折痕
,按上述方法不断操作下去…经过第2020次操作后得到的折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
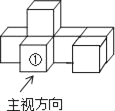
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
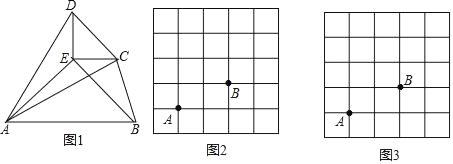
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图2,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图1,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进一批甲、乙两种玩具,已知![]() 件甲种玩具的进价与
件甲种玩具的进价与![]() 件乙种玩具的进价的和为
件乙种玩具的进价的和为![]() 元,
元,![]() 件甲种玩具的进价与
件甲种玩具的进价与![]() 件乙种玩具的进价的和为
件乙种玩具的进价的和为![]() 元.
元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过![]() 件,超出部分可以享受
件,超出部分可以享受![]() 折优惠,若购进
折优惠,若购进![]()
![]() 件甲种玩具需要花费
件甲种玩具需要花费![]() 元,请你写出
元,请你写出![]() 与
与![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com