
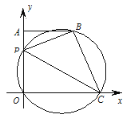
【题目】如图,在平面直角坐标系中,A(0,4),B(3,4),P 为线段 OA 上一动点,过 O,P,B 三点的圆交 x 轴正半轴于点 C,连结 AB, PC,BC,设 OP=m.
(1)求证:当 P 与 A 重合时,四边形 POCB 是矩形.
(2)连结 PB,求 tan∠BPC 的值.
(3)记该圆的圆心为 M,连结 OM,BM,当四边形 POMB 中有一组对边平行时,求所有满足条件的 m 的值.
(4)作点 O 关于 PC 的对称点O ,在点 P 的整个运动过程中,当点O 落在△APB 的内部 (含边界)时,请写出 m 的取值范围.
【答案】(1)见解析;(2)tan∠BPC=![]() ;(3)m=
;(3)m=![]() 或 m=
或 m=![]() ;(4)0≤m≤
;(4)0≤m≤![]() 或 m=
或 m=![]() .
.
【解析】
(1)由∠COA=90°可知PC为直径,所以∠PBC=90°,P、A重合时得3个直角,即证四边形POCB为矩形.
(2)题干已知的边长只有OA、AB,所以要把∠BPC转化到与OA、OB有关的三角形内.连接O,B,根据圆周角定理,得∠COB=∠BPC,又AB∥OC有∠ABP=∠COB,得∠BPC=∠ABO.
(3)分两种情况:①OP∥BM即BM⊥x轴,延长BM交x轴于N,根据垂径定理得ON=CN=3,设半径为r,利用Rt△CMN的三边关系列方程即可求出;②OM∥PB,根据圆周角定理和等腰三角形性质得到△BOM≌△COM,所以BO=CO=5,用m表示各条线段,再利用勾股定理列方程求得m的值.
(4)因为点O与点O'关于直线对称,所以∠PO'C=∠POC=90°,即点O'在圆上;考虑点P运动到特殊位置:①点O'与点O重合;②点O'落在AB上;③点O'与点B重合.算出对应的m值再考虑范围.
(1)∵∠COA=90°,∴PC是直径,∴∠PBC=90°.
∵A(0,4)B(3,4),∴AB⊥y轴,∴当A与P重合时,∠OPB=90°,∴四边形POCB是矩形;
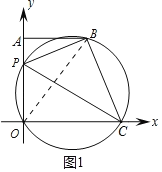
(2)连结OB,(如图1)
∴∠BPC=∠BOC.
∵AB∥OC,∴∠ABO=∠BOC,∴∠BPC=∠BOC=∠ABO,∴tan∠BPC=tan∠ABO![]() ;
;
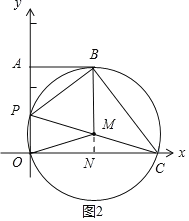
(3)∵PC为直径,∴M为PC中点.
①如图2,当OP∥BM时,延长BM交x轴于点N.
∵OP∥BM,∴BN⊥OC于N,∴ON=NC,四边形OABN是矩形,∴NC=ON=AB=3,BN=OA=4.
设⊙M半径为r,则BM=CM=PM=r,∴MN=BN﹣BM=4﹣r.
∵MN2+NC2=CM2,∴(4﹣r)2+32=r2
解得:r![]() ,∴MN=4
,∴MN=4![]() .
.
∵M、N分别为PC、OC中点,∴m=OP=2MN![]() ;
;
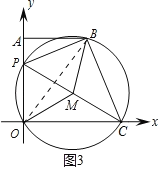
②如图3,当OM∥PB时,∠BOM=∠PBO.
∵∠PBO=∠PCO,∠PCO=∠MOC,∴∠OBM=∠BOM=∠MOC=∠MCO.
在△BOM与△COM中,∵∠BOM=∠COM,∠OBM=∠OCM,BM=CM,∴△BOM≌△COM(AAS),∴OC=OB![]() 5.
5.
∵AP=4﹣m,∴BP2=AP2+AB2=(4﹣m)2+32.
∵∠ABO=∠BOC=∠BPC,∠BAO=∠PBC=90°,∴△ABO∽△BPC,∴![]() ,∴PC
,∴PC![]() ,∴PC2
,∴PC2![]() BP2
BP2![]() [(4﹣m)2+32].
[(4﹣m)2+32].
又PC2=OP2+OC2=m2+52,∴![]() [(4﹣m)2+32]=m2+52
[(4﹣m)2+32]=m2+52
解得:m![]() 或m=10(舍去).
或m=10(舍去).
综上所述:m![]() 或m
或m![]() .
.
(4)∵点O与点O'关于直线对称,∴∠PO'C=∠POC=90°,即点O'在圆上.
当O'与O重合时,得:m=0;
当O'落在AB上时,得:m![]() ;
;
当O'与点B重合时,得:m![]() ;
;
∴0≤m![]() 或m
或m![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
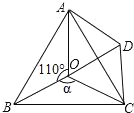
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
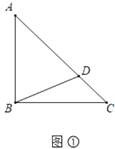
【题目】(问题提出)
(1)如图①,在等腰![]() 中,斜边
中,斜边![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,则
,则![]() 的最小值为 .
的最小值为 .
(问题探究)
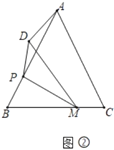
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,点
,点![]() 与点
与点![]() 对应,连接
对应,连接![]() ,求
,求![]() 的最小值.
的最小值.
(问题解决)
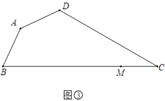
(3)如图③,四边形![]() 是规划中的休闲广场示意图,其中
是规划中的休闲广场示意图,其中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() .现计划在四边形
.现计划在四边形![]() 内选取一点
内选取一点![]() ,把
,把![]() 建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路
建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路![]() 、
、![]() ,从实用和美观的角度,要求满足
,从实用和美观的角度,要求满足![]() ,且景观绿化区面积足够大,即
,且景观绿化区面积足够大,即![]() 区域面积尽可能小.则在四边形
区域面积尽可能小.则在四边形![]() 内是否存在这样的点
内是否存在这样的点![]() ?若存在,请求出
?若存在,请求出![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
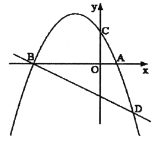
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校兴趣小组活动情况,随机抽取了部分同学进行调查,按A:艺术,B:科技,C:体育,D:其他四个项目进行统计,绘制了两幅统计图(均不完整),请根据统计图解答以下问题:
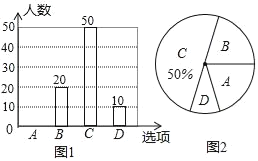
(1)本次接受问卷调查的共有 人:在扇形统计图中“D”选项所占的百分比为 ;
(2)扇形统计图中,“B”选项所对应扇形圆心角为 度;
(3)请补全条形统计图;
(4)若全校有2000人,请你估算一下全校喜欢艺术类学生的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,直线
点,直线![]() 交抛物线于点
交抛物线于点![]() ,并且,
,并且,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() 为抛物线上一动点,且在第二象限,顺次连接点
为抛物线上一动点,且在第二象限,顺次连接点![]() 、
、![]() 、
、![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
(3)在(2)中四边形![]() 面积最大的条件下,过点
面积最大的条件下,过点![]() 作直线平行于
作直线平行于![]() 轴,在这条直线上是否存在一个以
轴,在这条直线上是否存在一个以![]() 点为圆心,
点为圆心,![]() 为半径且与直线
为半径且与直线![]() 相切的圆?若存在,求出圆心
相切的圆?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() ,点
,点![]() 和点
和点![]() 是
是![]() 上关于直线
上关于直线![]() 对称的两个点,连接
对称的两个点,连接![]() 、
、![]() ,且
,且![]() ,直线
,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() 与线段
与线段![]() 的延长线相交于点
的延长线相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,且
,且![]() .
.

(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,满足
,满足![]() ,
,
①求证:![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
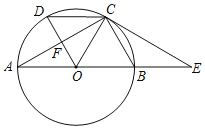
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com