
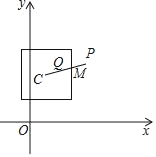
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжааФЮЊЕуCе§ЗНаЮЕФИїБпЗжБ№гыСНзјБъжсЦНааЃЌШєЕуPЪЧгыCВЛжиКЯЕФЕуЃЌЕуPЙигке§ЗНаЮЕФЗТЩфЕуQЕФЖЈвхШчЯТЃКЩшЩфЯпCPНЛе§ЗНаЮЕФБпгкЕуMЃЌШєЩфЯпCPЩЯДцдквЛЕуQЃЌТњзуCP+CQЃН2CMЃЌдђГЦQЮЊЕуPЙигке§ЗНаЮЕФЗТЩфЕуШчЭМЮЊЕуPЙигке§ЗНаЮЕФЗТЩфЕуQЕФЪОвтЭМЃЎ
ЬиБ№ЕиЃЌЕБЕуPгыжааФCжиКЯЪБЃЌЙцЖЈCPЃН0ЃЎ
ЃЈ1ЃЉЕБе§ЗНаЮЕФжааФЮЊдЕуOЃЌБпГЄЮЊ2ЪБЃЎ
ЂйЗжБ№ХаЖЯЕуFЃЈ2ЃЌ0ЃЉЃЌGЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌHЃЈ3ЃЌ3ЃЉЙигкИУе§ЗНаЮЕФЗТЩфЕуЪЧЗёДцдкЃПШєДцдкЃЌжБНгаДГіЦфЗТЩфЕуЕФзјБъЃЛ
ЃЉЃЌHЃЈ3ЃЌ3ЃЉЙигкИУе§ЗНаЮЕФЗТЩфЕуЪЧЗёДцдкЃПШєДцдкЃЌжБНгаДГіЦфЗТЩфЕуЕФзјБъЃЛ
ЂкШєЕуPдкжБЯпyЃНЉx+3ЩЯЃЌЧвЕуPЙигкИУе§ЗНаЮЕФЗТЩфЕуQДцдкЃЌЧѓЕуPЕФКсзјБъЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєе§ЗНаЮЕФжааФCдкxжсЩЯЃЌБпГЄЮЊ2ЃЌжБЯпyЃН![]() гыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌШєЯпЖЮABЩЯДцдкЕуPЃЌЪЙЕУЕуPЙигкИУе§ЗНаЮЕФЗТЩфЕуQдке§ЗНаЮЕФФкВПЃЌжБНгаДГіе§ЗНаЮЕФжааФCЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
гыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌШєЯпЖЮABЩЯДцдкЕуPЃЌЪЙЕУЕуPЙигкИУе§ЗНаЮЕФЗТЩфЕуQдке§ЗНаЮЕФФкВПЃЌжБНгаДГіе§ЗНаЮЕФжааФCЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЕу F ЕФЗТЩфЕузјБъЮЊЃЈ0ЃЌ0ЃЉЃЌЕу G ЕФЗТЩфЕузјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЂкЕу P дкжБЯп y=Љx+3 ЩЯЃЌЧвЕу P ЙигкИУе§ЗНаЮЕФЗТЩфЕу Q ДцдкЃЌЕу P ЕФКсзјБъЕФШЁжЕЗЖЮЇ1ЁмxЁм2ЃЛЃЈ2ЃЉТњзуЬѕМўЕФе§ЗНаЮЕФжааФ C ЕФКсзјБъЕФШЁжЕЗЖЮЇЮЊ 4Љ2
ЃЉЃЌЂкЕу P дкжБЯп y=Љx+3 ЩЯЃЌЧвЕу P ЙигкИУе§ЗНаЮЕФЗТЩфЕу Q ДцдкЃЌЕу P ЕФКсзјБъЕФШЁжЕЗЖЮЇ1ЁмxЁм2ЃЛЃЈ2ЃЉТњзуЬѕМўЕФе§ЗНаЮЕФжааФ C ЕФКсзјБъЕФШЁжЕЗЖЮЇЮЊ 4Љ2![]() ЁмxЁм5Љ
ЁмxЁм5Љ![]() Лђ 7Љ
Лђ 7Љ![]() ЁмxЁм8ЃЎ
ЁмxЁм8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнЕуPЙигке§ЗНаЮЕФЗТЩфЕуЕФЖЈвхПЩжЊЃКЕБЕудке§ЗНаЮABCDЃЈБпГЄЮЊ4ЁЂжааФЮЊдЕуOЃЉЕФФкВПЪБЃЈАќРЈе§ЗНаЮЕФБпЩЯЃЉгаЗТЩфЕуЃЌЙлВьЭМЯѓПЩжЊЃЌЕуFЃЌЕуGгаЗТЩфЕуЃЌИљОнЖЈвхМДПЩНтОіЮЪЬтЃЛ
ЂкШчЭМ2жаЃЌжБЯпy=-x+3НЛCDгкKЃЈ1ЃЌ2ЃЉЃЌНЛBCгкHЃЈ2ЃЌ1ЃЉЃЌЙлВьЭМЯѓМДПЩХаЖЯЃЛ
ЃЈ2ЃЉШчЭМ3жаЃЌгЩЬтвтAЃЈ0ЃЌ2![]() ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЎЧѓГіЫФИіЬиЪтЮЛжУЕФЕуCЕФзјБъМДПЩХаЖЯЃЛ
ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЎЧѓГіЫФИіЬиЪтЮЛжУЕФЕуCЕФзјБъМДПЩХаЖЯЃЛ
ЃЈ1ЃЉЂйШчЭМ 1 жаЃЌ
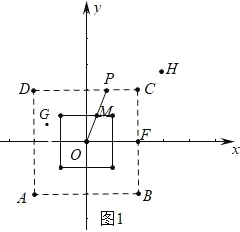
ИљОнЕуP Йигке§ЗНаЮЕФЗТЩфЕуЕФЖЈвхПЩжЊЃКЕБЕудке§ЗНаЮ ABCDЃЈБпГЄЮЊ 4 жааФЮЊдЕу OЃЉЕФФкВПЪБЃЈАќРЈе§ЗНаЮЕФБпЩЯЃЉЃЌгаЗТЩфЕуЃЌ
ЙлВьЭМЯѓПЩжЊЃЌЕу FЃЌЕу G гаЗТЩфЕуЃЌ
Еу F ЕФЗТЩфЕузјБъЮЊЃЈ0ЃЌ0ЃЉЃЌЕу G ЕФЗТЩфЕузјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЂкШчЭМ 2 жаЃЌ

ШчЭМжБЯп y=Љx+3 НЛ CD гк KЃЈ1ЃЌ2ЃЉЃЌНЛ BC гк HЃЈ2ЃЌ1ЃЉЃЌ
ЁрЕу P дкжБЯп y=Љx+3 ЩЯЃЌЧвЕу P ЙигкИУе§ЗНаЮЕФЗТЩфЕу Q ДцдкЃЌЕу P ЕФКсзјБъЕФШЁжЕЗЖЮЇЮЊ 1ЁмxЁм2ЃЛ
ЃЈ2ЃЉШчЭМ 3 жаЃЌгЩЬтвт AЃЈ0ЃЌ2![]() ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЎ
ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЎ

гЩЃЈ1ЃЉПЩжЊЕББпГЄЮЊ 4 ЕФе§ЗНаЮЕФЖЅЕу D дкЯпЖЮ AB ЩЯЪБЃЌDE=2ЃЌ
ЁпDEЁЮOAЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрEB=2![]() ЃЌOE=6Љ2
ЃЌOE=6Љ2![]() ЃЌ
ЃЌ
ЁрOC1=6Љ2![]() Љ2=4Љ2
Љ2=4Љ2![]() ЃЌ
ЃЌ
ЁрC1ЃЈ4Љ2![]() ЃЉ
ЃЉ
ЕББпГЄЮЊ 2 ЕФЖЅЕудкЯпЖЮ AB ЩЯЪБЃЌC2ЃЈ5Љ![]() ЃЌ0ЃЉЃЌC3ЃЈ7Љ
ЃЌ0ЃЉЃЌC3ЃЈ7Љ![]() ЃЉЃЌЕББпГЄЮЊ 4 ЕФе§ЗНаЮЕФБпОЙ§Еу B ЪБЃЌПЩЕУ C4ЃЈ8ЃЌ0ЃЉЃЌ
ЃЉЃЌЕББпГЄЮЊ 4 ЕФе§ЗНаЮЕФБпОЙ§Еу B ЪБЃЌПЩЕУ C4ЃЈ8ЃЌ0ЃЉЃЌ
ЙлВьЭМЯѓПЩжЊЃКТњзуЬѕМўЕФе§ЗНаЮЕФжааФ C ЕФКсзјБъЕФШЁжЕЗЖЮЇЮЊ 4Љ2![]() ЁмxЁм5Љ
ЁмxЁм5Љ ![]() Лђ 7Љ
Лђ 7Љ![]() ЁмxЁм8ЃЎ
ЁмxЁм8ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮжНЦЌABCDЃЌAB=9ЃЌBC=6ЃЌдкОиаЮБпЩЯгавЛЕуPЃЌЧвDP=3ЃЎНЋОиаЮжНЦЌелЕўЃЌЪЙЕуBгыЕуPжиКЯЃЌелКлЫљдкжБЯпНЛОиаЮСНБпгкЕуEЃЌFЃЌдђEFГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
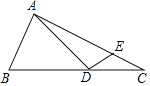
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=3ЃЌAC=6![]() ЃЌЕуDЃЌEЗжБ№ЪЧБпBCЃЌACЩЯЕФЖЏЕуЃЌдђDA+DEЕФзюаЁжЕЮЊ_____ЃЎ
ЃЌЕуDЃЌEЗжБ№ЪЧБпBCЃЌACЩЯЕФЖЏЕуЃЌдђDA+DEЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇЯАИХТЪЕФПЮЬУЩЯЃЌРЯЪІЬсГіЮЪЬтЃКвЛПкДќзАгаГ§беЩЋЭтОљЯрЭЌЕФ2ИіКьЧђ1ИіАзЧђКЭ1ИіРКЧђЃЌаЁИеКЭаЁУїЯыЭЈЙ§УўЧђРДОіЖЈЫШЅПДЕчгАЃЌЭЌбЇМзЩшМЦСЫШчЯТЕФЗНАИЃКЕквЛДЮЫцЛњДгПкДќжаУўГівЛЧђЃЈВЛЗХЛиЃЉЃЛЕкЖўДЮдйШЮвтУўГівЛЧђЃЌСНШЫЪЄИКЙцдђШчЯТЃКУўЕНЁАвЛКьвЛАзЁБЃЌдђаЁИеПДЕчгАЃЛУўЕНЁАвЛАзвЛРЖЁБЃЌдђаЁУїПДЕчгАЃЎ
ЃЈ1ЃЉЭЌбЇМзЕФЗНАИЙЋЦНТ№ЃПЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЫЕУїЃЛ
ЃЈ2ЃЉФуШєШЯЮЊетИіЗНАИВЛЙЋЦНЃЌФЧУДЧыФуИФБфвЛЯТЙцдђЃЌЩшМЦвЛИіЙЋЦНЕФЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
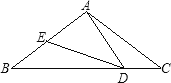
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌAB=AC=5ЃЌBC=8ЃЌDЃЌEЗжБ№ЮЊBCЃЌABБпЩЯвЛЕуЃЌЁЯADE=ЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBDEЁзЁїCADЃЛ
ЃЈ2ЃЉШєCD=2ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
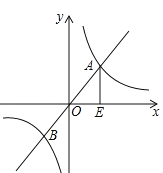
ЁОЬтФПЁПШчЭМЃЌвбжЊКЏЪ§y=2xКЭКЏЪ§y=![]() ЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌШєЁїAOEЕФУцЛ§ЮЊ4ЃЌPЪЧзјБъЦНУцЩЯЕФЕуЃЌЧввдЕуBЁЂOЁЂEЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌдђk= ЃЌТњзуЬѕМўЕФPЕузјБъЪЧ ЃЎ
ЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌШєЁїAOEЕФУцЛ§ЮЊ4ЃЌPЪЧзјБъЦНУцЩЯЕФЕуЃЌЧввдЕуBЁЂOЁЂEЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌдђk= ЃЌТњзуЬѕМўЕФPЕузјБъЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїМввћЫЎЛњжадгаЫЎЕФЮТЖШЮЊ20ЁцЃЌЭЈЕчПЊЛњКѓЃЌвћЫЎЛњздЖЏПЊЪММгШШ[ДЫЙ§ГЬжаЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉТњзувЛДЮКЏЪ§ЙиЯЕ]ЃЌЕБМгШШЕН100ЁцЪБздЖЏЭЃжЙМгШШЃЌЫцКѓЫЎЮТПЊЪМЯТНЕ[ДЫЙ§ГЬжаЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉГЩЗДБШР§ЙиЯЕ]ЃЌЕБЫЎЮТНЕжС20ЁцЪБЃЌвћЫЎЛњгжздЖЏПЊЪММгШШЁЃЌжиИДЩЯЪіГЬађЃЈШчЭМЫљЪОЃЉЃЌИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБ0ЁмxЁм8ЪБЃЌЧѓЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЭМжаtЕФжЕЃЛ
ЃЈ3ЃЉШєаЁУїдкЭЈЕчПЊЛњКѓМДЭтГіЩЂВНЃЌЧыФудЄВтаЁУїЩЂВН45ЗжжгЛиЕНМвЪБЃЌвћЫЎЛњФкЕФЮТЖШдМЮЊЖрЩйЁцЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпгыжБЯпЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаЫЕЗЈЃК
ЂйЕБ0ЃМxЃМ2ЪБЃЌ y1ЃОy2ЃЛЂкy1ЫцxЕФдіДѓЖјдіДѓЕФШЁжЕЗЖЮЇЪЧxЃМ2ЃЛЂлЪЙЕУy2Дѓгк4ЕФxжЕВЛДцдкЃЛЂмШєy1=2ЃЌдђx=2Љ![]() Лђx=1ЃЎЦфжае§ШЗЕФгаЃЈ ЃЉ
Лђx=1ЃЎЦфжае§ШЗЕФгаЃЈ ЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊГЃЪ§aЃЈaЪЧећЪ§ЃЉТњзуЯТУцСНИівЊЧѓЃК
ЂйЙигкxЕФвЛдЊЖўДЮЗНГЬax2+3xЉ1=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЂкЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓдкЖўЃЌЫФЯѓЯоЃЎ
ЕФЭМЯѓдкЖўЃЌЫФЯѓЯоЃЎ
ЃЈ1ЃЉЧѓaЕФжЕЃЛ
ЃЈ2ЃЉдкЫљИјжБНЧзјБъЯЕжагУУшЕуЗЈЛГіy=![]() ЕФЭМЯѓЃЌВЂИљОнЭМЯѓаДГіЃК
ЕФЭМЯѓЃЌВЂИљОнЭМЯѓаДГіЃК
ЕБxЃО4ЪБЃЌyЕФШЁжЕЗЖЮЇ ЃЛ
ЕБyЃМ1ЪБЃЌxЕФШЁжЕЗЖЮЇЪЧЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com