
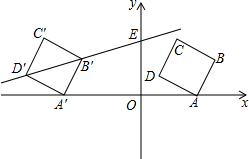
���� ��1������D��DG��x���ڵ�G��BF��x���ڵ�F������ASA�����ɵá�ADG�ա�BAF���ʿɵó������ꣻ
��2������t��ʾ��ƽ�ƺ�B�䣬D������꣬�ٸ��ݷ���������ͼ���ϵ�������ص����t��ֵ�����ô���ϵ������������������Ľ���ʽ���ɣ�
��3�������ô���ϵ�������ֱ��B��D��Ľ���ʽ���ʿɵó�E�����꣬����P��a��0����Q��x��-$\frac{6}{x}$������B��EΪ�Խ��ߺͱ���������������ۣ�
��� 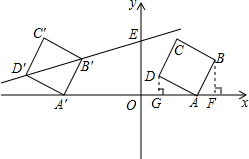 �⣺��1������D��DG��x���ڵ�G��BF��x���ڵ㣬
�⣺��1������D��DG��x���ڵ�G��BF��x���ڵ㣬
�ߡ�DAG+��ADG=90�㣬��DAG+��BAF=90�㣬��BAF+��ABF=90�㣬
���DAG=��ABF����ADG=��BAF��
�ڡ�ADG���BAF�У�
$\left\{\begin{array}{l}��DAG=��ABF\\ AD=AB\\��ADG=��BAF\end{array}\right.$��
���ADG�ա�BAF��ASA����
��DG=AF=1��AG=BF=3-1=2��
��B��4��2����
��2����B��4��2����D��1��1����
��t���B�䣨4-t��2����D�䣨1-t��1����
����t��������ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ�
��2��4-t��=1-t�����t=7��
��B�䣨-3��2����D�䣨-6��1����
��k=2����-3��=-6��
�෴���������Ľ���ʽΪy=-$\frac{6}{x}$��
��3�����ڣ�
��ֱ��B��D��Ľ���ʽΪy=kx+b��k��0����
��B�䣨-3��2����D�䣨-6��1����
��$\left\{\begin{array}{l}2=-3k+b\\ 1=-6k+b\end{array}\right.$��
���$\left\{\begin{array}{l}k=\frac{1}{3}\\ b=3\end{array}\right.$��
��ֱ��B��D��Ľ���ʽΪy=$\frac{1}{3}$x+3��
��E��0��3����
��P��a��0����Q��x��-$\frac{6}{x}$����
��B��EΪ�Խ���ʱ��$\frac{a+x}{2}$=$\frac{-3}{2}$��$\frac{-\frac{6}{x}}{2}$=$\frac{2+3}{2}$�����a=-$\frac{9}{5}$��x=-$\frac{6}{5}$��
��P��-$\frac{9}{5}$��0����Q��-$\frac{6}{5}$��5����
��B��EΪ��ʱ����Q��������Ϊ-1����ʱQ��-1��6����P��9��0����
������ʾ��P��-$\frac{9}{5}$��0����Q��-$\frac{6}{5}$��5����Q��-1��6����P��9��0����
���� ���⿼����Ƿ����������ۺ��⣬�漰���ô���ϵ������һ�κ����������������Ľ���ʽ�������ε����ʵ�֪ʶ���ڽ��3��ʱҪע����з������ۣ�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 һ����ˮ�ܵĽ�����ͼ��ʾ����֪��ˮ�ܵ�ˮ��CD=4��ˮ���AB=16�������Բ�뾶OB�ǣ�������
һ����ˮ�ܵĽ�����ͼ��ʾ����֪��ˮ�ܵ�ˮ��CD=4��ˮ���AB=16�������Բ�뾶OB�ǣ�������| A�� | 8 | B�� | 10 | C�� | 12 | D�� | $8\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6a3b=3a2•2ab | B�� | ��x+2����x-2��=x2-4 | ||
| C�� | 2x2+4x-3=2x��x+2��-3 | D�� | ax-ay=a��x-y�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
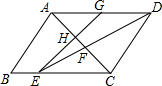 ��ͼ����֪?ABCD��DEƽ�֡�ADC�ֱ�BC��AC�ڵ�E��F��G��AD�е㣬EG��AC�ڵ�H����AB=4��AD=6����
��ͼ����֪?ABCD��DEƽ�֡�ADC�ֱ�BC��AC�ڵ�E��F��G��AD�е㣬EG��AC�ڵ�H����AB=4��AD=6�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com