
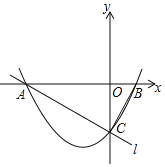
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=![]() x2+
x2+![]() x��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����A��C���㣬����BC��
x��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����A��C���㣬����BC��
��1����ֱ��l�Ľ���ʽ��
��2����ֱ��x=m��m��0������������ڵ��������ڽ��ڵ�E����ֱ��l���ڵ�D������OD����OD��ACʱ�����߶�DE�ij���
��3��ȡ��G��0����1��������AG���ڵ�һ�����ڵ��������ϣ��Ƿ���ڵ�P��ʹ��BAP=��BCO����BAG�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() ����2��DE=
����2��DE=![]() ����3�����ڵ�P��
����3�����ڵ�P��![]() ��
��![]() ����ʹ��BAP=��BCO����BAG�����ɼ�����.
����ʹ��BAP=��BCO����BAG�����ɼ�����.
��������
��1��������Ŀ�еĺ�������ʽ������õ�A�͵�C�����꣬�Ӷ��������ֱ��l�ĺ�������ʽ��
��2�����������������ʵĸ����ߣ��������������ƺ��ɶ������Խ���⣻
��3���������⻭����Ӧ��ͼ�Σ�Ȼ�����������Ǻ���������á�OAC=��OCB��Ȼ�������Ŀ�е�������ͼ�Σ�����������Ǻ������ɶ������ɽ���⣮
��1����������y=![]() x2+
x2+![]() x-2��
x-2��
�൱y=0ʱ����x1=1��x2=-4����x=0ʱ��y=-2��
��������y=![]() x2+
x2+![]() x-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
x-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
���A��������-4��0������B��1��0������C��0��-2����
��ֱ��l����A��C���㣬��ֱ��l�ĺ�������ʽΪy=kx+b��
![]() ����
����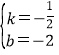 ��
��
��ֱ��l�ĺ�������ʽΪy=![]() x2��
x2��
��2��ֱ��ED��x�ύ�ڵ�F����ͼ1��ʾ��
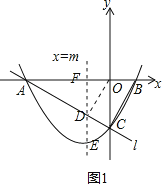
�ɣ�1���ɵã�
AO=4��OC=2����AOC=90�㣬
��AC=2![]() ��
��
��OD=![]() ��
��
��OD��AC��OA��OC����OAD=��CAO��
���AOD�ס�ACO��
��![]() ��
��
��![]() ����AD=
����AD=![]() ��
��
��EF��x�ᣬ��ADC=90�㣬
��EF��OC��
���ADF�ס�ACO��
��![]() ��
��
��ã�AF=![]() ��DF=
��DF=![]() ��
��
��OF=4-![]() =
=![]() ��
��
��m=-![]() ��
��
��m=-![]() ʱ��y=
ʱ��y=![]() ����
����![]() ��2+
��2+![]() ����-
����-![]() ��-2=-
��-2=-![]() ��
��
��EF=![]() ��
��
��DE=EF-FD=![]()
![]() ��
��![]() ��
��
��3�����ڵ�P��ʹ��BAP=��BCO-��BAG��
���ɣ���GM��AC�ڵ�M����PN��x���ڵ�N����ͼ2��ʾ��
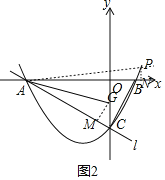
�ߵ�A��-4��0������B��1��0������C��0��-2����
��OA=4��OB=1��OC=2��
��tan��OAC=![]() ��tan��OCB=
��tan��OCB=![]() ��AC=2
��AC=2![]() ��
��
���OAC=��OCB��
�ߡ�BAP=��BCO-��BAG����GAM=��OAC-��BAG��
���BAP=��GAM��
�ߵ�G��0��-1����AC=2![]() ��OA=4��
��OA=4��
��OG=1��GC=1��
��AG=![]() ��
��![]() ����
����![]() ��
��
��ã�GM=![]() ��
��
��AM=![]() =
=![]() ��
��
��tan��GAM=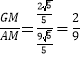 ��
��
��tan��PAN=![]() ��
��
���P��������n��![]() n2+
n2+![]() n-2����
n-2����
��AN=4+n��PN=![]() n2+
n2+![]() n-2��
n-2��
��![]() ��
��
��ã�n1=![]() ��n2=-4����ȥ����
��n2=-4����ȥ����
��n=![]() ʱ��
ʱ��![]() n2+
n2+![]() n-2=
n-2=![]() ��
��
���P��������![]() ��
��![]() ����
����
�����ڵ�P��![]() ��
��![]() ����ʹ��BAP=��BCO-��BAG��
����ʹ��BAP=��BCO-��BAG��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������У��ȫ���ܵ�ȫ���Ĺ㷺��ע����Ϫ��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ� ���������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1������ͳ��ͼ�С������˽⡱���ֶ�Ӧ���ε�Բ�Ľ�Ϊ�����ȣ��벹ȫ����ͳ��ͼ��
��2�����ﵽ���˽⡱�̶ȵ�������1��������2��Ů�����ﵽ�����˽⡱�̶ȵ�������1��������1��Ů�������ֱ�Ӵﵽ���˽⡱�̶Ⱥ͡����˽⡱�̶ȵ����зֱ��ȡ1�˲μ�У֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ֪��y=��![]() x+m�뷴��������y=
x+m�뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ���A��B���㣨��A�ڵ�B����ࣩ���ֱ���x��y�ύ�ڵ�C��D��AE��x����E��
��ͼ���ڵ�һ�����ڽ���A��B���㣨��A�ڵ�B����ࣩ���ֱ���x��y�ύ�ڵ�C��D��AE��x����E��
��1����OECE=12����k��ֵ��
��2����ͼ2����BF��y����F����֤��EF��CD��
��3���ڣ�1����2���������£�EF=![]() �� AB=2
�� AB=2![]() ��P��x���������ϵ�һ�㣬����PAB����PΪֱ�Ƕ���ĵ���ֱ�������Σ���P������꣮
��P��x���������ϵ�һ�㣬����PAB����PΪֱ�Ƕ���ĵ���ֱ�������Σ���P������꣮
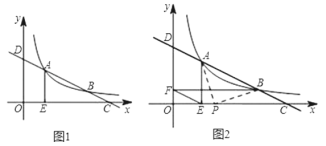
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A��90�㣬AD��BC��BE��CD��E��AD���ӳ�����F��DC��2AD��AB��BE��
��1����֤��AD��DE��
��2����֤���ı���BCFD�����Σ�
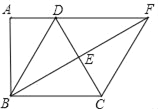
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC=90�㣬AB=AD������BD����E��AB�ϣ�����BDE=15�㣬DE=4![]() ��DC=2
��DC=2![]() ��
��
��1����BE�ij���
��2�����ı���DEBC�������
��ע�⣺�����еļ�����̺ͽ�����������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�г���ɫ���������ͬ��5��С�����к���3��������2����
��1�����ȴӴ���ȡ��x��x��0���������ٴӴ������������1������������������Ϊ�¼�A����AΪ��Ȼ�¼�����x��ֵΪ�� ����
��2�����Ӵ����������2�������ú������1�����û���״ͼ���б���������¼��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���ABC=120�㣬�������۵���ʹ��Aǡ�����ڶԽ���BD�ϵĵ�G��������B��D�غϣ����ۺ�ΪEF����DG=2��BG=6����BE�ij�Ϊ______��
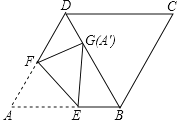
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����κ�����ͼ�������ʺ���ʦ��ѧ����˵��![]() ��ͼ���һЩ���ʣ�С��˵�����˺���ͼ�����ϣ��ҶԳ�����
��ͼ���һЩ���ʣ�С��˵�����˺���ͼ�����ϣ��ҶԳ�����![]() ����С��˵�����˺����϶���x�����������㡱��С��˵�����˺�����y��Ľ�������Ϊ��0��-3������Сǿ˵�����˺�������Сֵ��
����С��˵�����˺����϶���x�����������㡱��С��˵�����˺�����y��Ľ�������Ϊ��0��-3������Сǿ˵�����˺�������Сֵ�� ![]() ��������������λͬѧ˭˵�Ľ����Ǵ���������� ��
��������������λͬѧ˭˵�Ľ����Ǵ���������� ��
A. С�� B. С�� C. С�� D. Сǿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+2x��1��
��1��д�����Ķ������ꣻ
��2����xȡ��ֵʱ��y��x�����������
��3����xȡ��ֵʱy��ֵ����0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com