
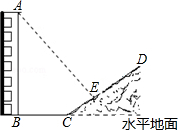
 如图,一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长BC=25米,落在坡面上的影长CE=20米,已知小丽测得同一时刻1米高的竹竿在水平地面上的影长为0.8米,求楼房AB的高.($\sqrt{3}$≈1.7)
如图,一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长BC=25米,落在坡面上的影长CE=20米,已知小丽测得同一时刻1米高的竹竿在水平地面上的影长为0.8米,求楼房AB的高.($\sqrt{3}$≈1.7) 分析 延长AE交BC的延长线于F,作EG⊥CF,根据CE=20米,∠ECG=30°,分别求出EG、CG的长度,又根据竹竿在水平面上的影长,可得EG:GF=1:0.8,AB:BF=1:0.8,代入求出BF、AB的长度即可.
解答 解:延长AE交BC的延长线于F,作EG⊥CF,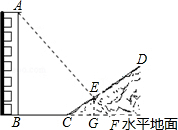
∵CE=20米,∠ECG=30°,
∴EG=10米,CG=10$\sqrt{3}$≈17(米),
又∵$\frac{EG}{GF}=\frac{1}{0.8}$,
∴$\frac{10}{GF}=\frac{1}{0.8}$,
∴GF=8米,
∴BF=25+17+8=50(米),
∵$\frac{AB}{BF}=\frac{1}{0.8}$,
∴$\frac{AB}{50}=\frac{1}{0.8}$,
∴AB=62.5米.
即楼房的高度约为62.5米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目所给的角构造直角三角形,利用三角函数的知识求解.


科目:初中数学 来源: 题型:解答题
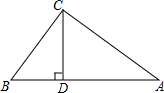 如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}=\frac{CD}{BD}$
如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}=\frac{CD}{BD}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四条边都相等的四边形是矩形 | |
| B. | 菱形的对角线相等 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 对角线相等且互相平分的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com