
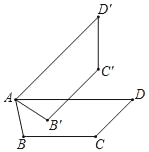
【题目】如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(![]() ≈1.7)
≈1.7)
A. 21cmB. 42cmC. 51cmD. 60cm
【答案】B
【解析】
设AD与B′C′交于G,过B′作B′F⊥AD于F,延长D′C′交AD于E,根据旋转的性质得到∠D′=∠D=45°,AB′=AB,C′D′=CD=60cm,根据等腰直角三角形的性质得到C′E=GE,求得AG=C′D′=60,解直角三角形即可得到结论.
解:设AD与B′C′交于G,
过B′作B′F⊥AD于F,延长D′C′交AD于E,
由旋转的性质得,∠D′=∠D=45°,AB′=AB,C′D′=CD=60cm,
∵D′C′⊥AD,
∴∠AED′=90°,
∴△AED′是等腰直角三角形,
∴AE=D′E,
∵AD∥BC,
∴AD′∥B′C′,
∴△GC′E是等腰直角三角形,
∴C′E=GE,
∴AG=C′D′=60,
∵∠FGB′=∠C′GE=45°,
∴FG=FB′,
∵∠DAB′=30°,
∴AF=![]() FB′,
FB′,
∴FB′+![]() FB′=60,
FB′=60,
∴FB′=30(![]() ﹣1),
﹣1),
∴AB=AB′=2FB′=60(![]() ﹣1)=42cm.
﹣1)=42cm.
故选:B.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】在湖边高出水面40m的山顶A处看见一架无人机停留在湖面上空某处,观察到无人机底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则无人机底部P距离湖面的高度是( )
A. (40![]() +40)mB. (40
+40)mB. (40![]() +80)mC. (50
+80)mC. (50![]() +100)mD. (50
+100)mD. (50![]() +50)m
+50)m
查看答案和解析>>
科目:初中数学 来源: 题型:
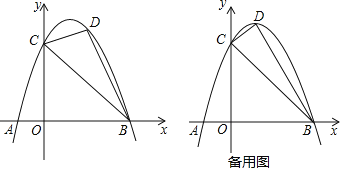
【题目】如图,二次函数![]() 的图象交x轴于A、B两点
的图象交x轴于A、B两点![]() 其中点A在点B的左侧
其中点A在点B的左侧![]() ,交y轴正半轴于点C,且
,交y轴正半轴于点C,且![]() ,点D在该函数的第一象限内的图象上.
,点D在该函数的第一象限内的图象上.
![]() 求点A、点B的坐标;
求点A、点B的坐标;
![]() 若
若![]() 的最大面积为
的最大面积为![]() 平方单位,求点D的坐标及二次函数的关系式;
平方单位,求点D的坐标及二次函数的关系式;
![]() 若点D为该函数图象的顶点,且
若点D为该函数图象的顶点,且![]() 是直角三角形,求此二次函数的关系式.
是直角三角形,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
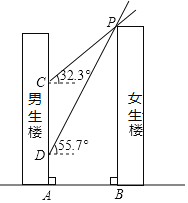
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
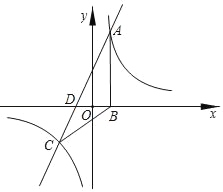
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、C两点,与x轴交于点D,过点A作AB⊥x轴于点B,点O是线BD的中点,AD=2
(k≠0)的图象交于A、C两点,与x轴交于点D,过点A作AB⊥x轴于点B,点O是线BD的中点,AD=2![]() ,cos∠ADB=
,cos∠ADB=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当x为何值时,y1≥y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
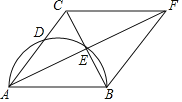
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使
,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使![]() ,连接FB,FC.
,连接FB,FC.
![]() 求证:四边形ABFC是菱形;
求证:四边形ABFC是菱形;
![]() 若
若![]() ,
,![]() ,求半圆和菱形ABFC的面积.
,求半圆和菱形ABFC的面积.
![]() 只用一把无刻度的直尺,作出菱形AB上的高CH.
只用一把无刻度的直尺,作出菱形AB上的高CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com