
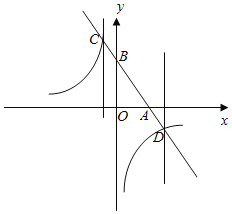
【题目】如图,一次函数y1=kx+b的图象分别交x轴,y轴于A,B两点,交反比例函数y2=![]() 的图象于C,D两点,B(0,3),D(2,﹣1).
的图象于C,D两点,B(0,3),D(2,﹣1).
(1)求一次函数与反比例函数的表达式;
(2)请直接写出当y2≥y1时,x的取值范围;
(3)点E为反比例函数y2=![]() 的图象上一点,横坐标为m,若将点E向右平移2个单位后刚好落在一次函数y1=kx+b的图象上,求m的值.
的图象上一点,横坐标为m,若将点E向右平移2个单位后刚好落在一次函数y1=kx+b的图象上,求m的值.
【答案】(1)一次函数的关系式为y=﹣2x+3;反比例函数的关系式为y=﹣![]() ;(2)﹣
;(2)﹣![]() <x<0或x>2;(3)
<x<0或x>2;(3)![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解一次函数与反比例函数的解析式即可;
(2)先把两个函数解析式联立求解![]() 的坐标,再根据图像直接写出不等式的解集即可;
的坐标,再根据图像直接写出不等式的解集即可;
(3)利用含![]() 的代数式分别表示
的代数式分别表示![]() 的坐标,利用平移的性质的两点的纵坐标不变,列方程求解即可.
的坐标,利用平移的性质的两点的纵坐标不变,列方程求解即可.
解:(1)把B(0,3),D(2,﹣1)代入一次函数y1=kx+b得,
![]() ,
,
解得:![]()
∴一次函数的关系式为y=﹣2x+3,
把D(2,﹣1)代入反比例函数关系式得,a=2×(﹣1)=﹣2,
∴反比例函数的关系式为y=﹣![]() ;
;
(2)由题意得,
 ,
,
解得: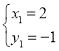 ,
,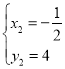 ,
,
∵D(2,﹣1),
∴C(﹣![]() ,4),
,4),
根据图象可知,当y2≥y1时,x的取值范围为﹣![]() <x<0或x>2.
<x<0或x>2.
(3)设平移后落在y=﹣2x+3上的对应点为E′,
则E(m,﹣![]() ),E′(m+2,﹣2m﹣1)
),E′(m+2,﹣2m﹣1)
因此有:﹣![]() =﹣2m+1,
=﹣2m+1,
解得,m1=![]() ,m2=
,m2=![]() ,
,
经检验,均符合题意,
故m的值为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
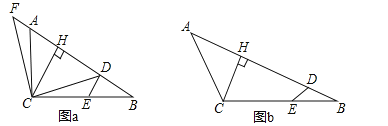
【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A在第一象限,点B在x轴的正半轴上,点G为△OAB的重心,连接BG并延长,交OA于点C,反比例函数y=![]() (k>0)的图象经过C,G两点.若△AOB的面积为6,则k的值为( )
(k>0)的图象经过C,G两点.若△AOB的面积为6,则k的值为( )
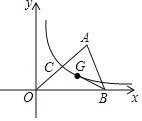
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P1(x1,y1)、P2(x2,y2),一定能使![]() <0成立的是( )
<0成立的是( )
A.y=3x﹣1(x<0)B.y=﹣x2+2x﹣1(x>0)
C.y=﹣![]() (x>0)D.y=x2﹣4x+1(x<0)
(x>0)D.y=x2﹣4x+1(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
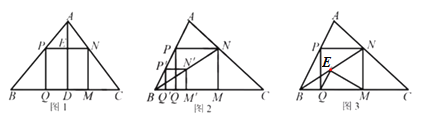
(1)温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB, AC上,若BC=6,AD=4,求正方形PQMN的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.
(3)推理:证明图2中的四边形PQMN 是正方形.
(4)拓展:在(2)的条件下,于波利业线B N上截取NE=NM,连结EQ,EM(如图3).当tan∠NBM=![]() 时,猜想∠QEM的度数,并尝试证明.
时,猜想∠QEM的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
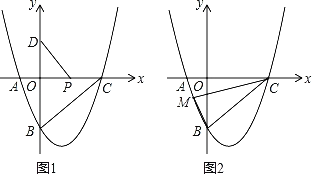
【题目】二次函数y=ax2﹣2x+c的图象与x轴交于A、C两点,点C(3,0),与y轴交于点B(0,﹣3).
(1)a= ,c= ;
(2)如图1,P是x轴上一动点,点D(0,1)在y轴上,连接PD,求![]() PD+PC的最小值;
PD+PC的最小值;
(3)如图2,点M在抛物线上,若S△MBC=3,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com