Question

9．在平面直角坐标系中，二次函数y=x²+bx+c的图象经过点（3，0）、（2，-3），若这个二次函数图象的顶点是点P，与y轴交点是点Q，求△OPQ的面积．

Answer 1

分析 先利用待定系数法求二次函数的解析式，利用配方法求顶点P的坐标，及Q的坐标，画出图象，根据△OPQ的位置求面积．

解答 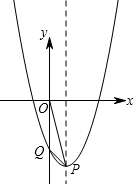解：把（3，0）、（2，-3）代入y=x²+bx+c得，
$\left\{\begin{array}{l}{9+3b+c=0}\\{4+2b+c=-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$，
∴二次函数解析式为：y=x²-2x-3，
y=x²-2x-3=（x-1）²-4，
∴P（1，-4），Q（0，-3），
则△OPQ的面积=$\frac{1}{2}$×OQ×1=$\frac{1}{2}$×3×1=$\frac{3}{2}$．

点评 本题考查了利用待定系数法求二次函数的解析式及抛物线与坐标轴组成的三角形的面积，先确定其三角形的各点的坐标，观察其位置，直接代入面积公式或利用和、差求解．