
【题目】如图所示,![]() 分别切
分别切![]() 的三边
的三边![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() .
.
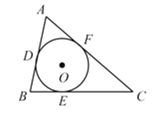
(1)求![]() 的长;
的长;
(2)求![]() 的半径长.
的半径长.
【答案】(1)4;(2)2
【解析】
(1)设AD=x,根据切线长定理得到AF=AD,BE=BD,CE=CF,根据关系式列得方程解答即可;
(2)连接OD、OE、OF、OA、OB、OC,将△ABC分为三个三角形:△AOB、△BOC、△AOC,再用面积法求得半径即可.
解:(1)设 ![]() ,
,
![]() 分别切
分别切 ![]() 的三边
的三边 ![]() 、
、![]() 、
、![]() 于点
于点 ![]() 、
、![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即 ![]() ,得
,得 ![]() ,
,
![]() 的长为
的长为 ![]() .
.
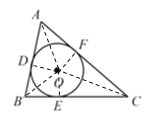
(2)如图,连接OD、OE、OF、OA、OB、OC,
则OD⊥AB,OE⊥BC,OF⊥AC,且OD=OE=OF=2,
∵![]() ,
,![]() ,
,![]() ,
,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠B是直角,
∴△ABC的面积=![]() ,
,
∴![]() ,
,
∴OD=2,即![]() 的半径长为2.
的半径长为2.


科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为__________.
边的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关注数学文化:古希腊的几何学家海伦在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中,给出了如下公式:若一个三角形的三边长分别为a,b,c,记p=![]() ,则三角形的面积S=
,则三角形的面积S=![]() (海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式:
(海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式: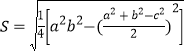 .海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
.海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
若△ABC的三边长分别为5,6,7,△DEF的三边长分别为![]() ,
,![]() ,
,![]() ,请选择合适的公式分别求出△ABC和△DEF的面积.
,请选择合适的公式分别求出△ABC和△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
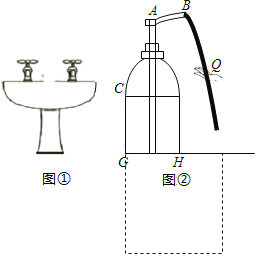
【题目】同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣![]() .洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若学校组织学生去南京进行研学实践活动,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若学校组织学生去南京进行研学实践活动,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12![]() B.12
B.12![]() C.6
C.6![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对的直角边与
所对的直角边与![]() 的斜边恰好重合。以
的斜边恰好重合。以![]() 为直径的圆经过点C,且与
为直径的圆经过点C,且与![]() 相交于点E,连接
相交于点E,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于F.
于F.
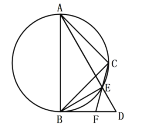
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 与
与![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com