
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为__________.
边的长为__________.

【答案】4
【解析】
当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,结合图象可得△AOP面积最大为3,得到AB与BC的积为12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,得到AB与BC的和为7,构造关于AB的一元二方程可求解.
解:当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3.
∴![]() AB
AB![]() BC=3,即ABBC=12.
BC=3,即ABBC=12.
当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,
∴AB+BC=7.
则BC=7-AB,代入ABBC=12,得AB2-7AB+12=0,解得AB=4或3,
因为AB<AD,即AB<BC,
所以AB=3,BC=4
∴AD=BC=4.
故答案为:4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
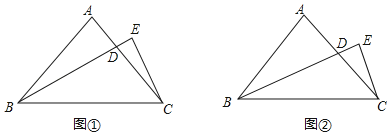
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过点C作CE⊥BD,交BD的延长线于点E,如图①.
(1)求证:ADCD=BDDE;
(2)若BD是边AC的中线,如图②,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
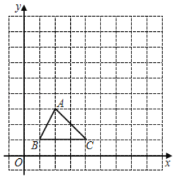
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系.
的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系.![]() 的三个顶点均在格点上.
的三个顶点均在格点上.
(1)若将![]() 沿x轴对折得到
沿x轴对折得到![]() ,则
,则![]() 的坐标为_______;
的坐标为_______;
(2)以点B为位似中心,将![]() 各边放大为原来的2倍,得到
各边放大为原来的2倍,得到![]() ,请在这个网格中画出
,请在这个网格中画出![]() ;
;
(3)在(2)的条件下,若小明蒙上眼睛在一定距离外,向![]() 的正方形网格内掷小石子,则刚好掷入
的正方形网格内掷小石子,则刚好掷入![]() 的概率是多少?(未掷入图形内则不计次数,重掷一次)
的概率是多少?(未掷入图形内则不计次数,重掷一次)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点,学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大玉米”的高度他们制订了测量方案,并利用课余时间完成了实地测量,测量项目及结果如下表
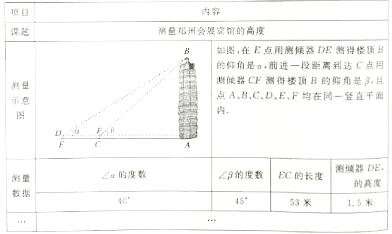
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
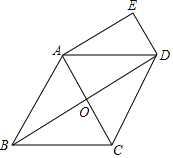
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2![]() ,AC=2,求四边形AODE的周长.
,AC=2,求四边形AODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
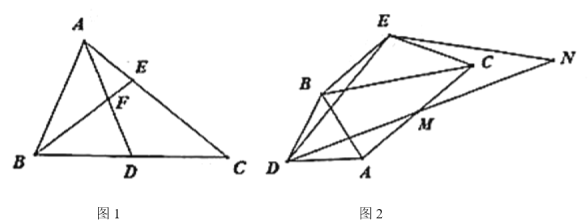
【题目】如图1,在![]() 中,
中,![]() 分别为
分别为![]() 上一点,且
上一点,且![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,将
,将![]() 绕
绕![]() 顺时针旋转至如图2所示位置(
顺时针旋转至如图2所示位置(![]() 不动),连
不动),连![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,
,![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知不等臂跷跷板AB长为3米,跷跷板AB的支撑点O到地面上的点H的距高OH=0.6米。当跷跷板AB的一个端点A碰到地面时,AB与地面上的直线AH的夹角∠OAH的度数为30°.

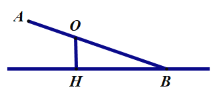
(1)当AB的另一个端点B碰到地面时(如右图),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?
(2)当AB的另一个端点B碰到地面时(如右图),点A到直线BH的距离是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com