
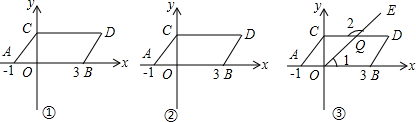
���� ��1����ͼ��ֱ�ӿ���д����������꣬��ƽ���ı��������ʽ���㼴�ɣ�
��2������y���ϴ���P��0��b���㣬ʹS��PAB=S�ı���ABDC���з��̣����b��
��3�������жϣ���֤����
��� ��1���⣺C��0��2��D��4��2��
S�ı���ABDC=|AB|•|CO|
=4��2
=8��
��2���⣺����y���ϴ���P��0��b���㣬��S��PAB=S�ı���ABDC
$\frac{1}{2}$|AB|•|b|=8��
b=��4��
��P��0��4����P��0��-4����
��3���⣺����ȷ
��CD����ABƽ�����õ��ģ�
��CD��AB��
���1=��EQD����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�2+��EQD=180�㣬
���1+��2=180�㣨�����180����
���� ���⿼��ƽ���й�֪ʶ��ƽ�ƵĻ��������ǣ���ƽ�Ʋ��ı�ͼ�ε���״�ʹ�С���ھ���ƽ�ƣ���Ӧ���������߶�ƽ������ȣ���Ӧ�߶�ƽ������ȣ���Ӧ����ȣ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
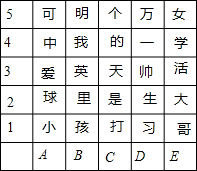 ��ͼ����������25�����֣��ã�C��3����ʾ���족��ô������Ҫ�����л����һ��ʲô��������д������
��ͼ����������25�����֣��ã�C��3����ʾ���족��ô������Ҫ�����л����һ��ʲô��������д�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
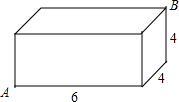 ��ͼ����һ��������ij��������߷ֱ��� 6��4��5���ڵ���A����һֻ���ϣ�����Ե�����������B����ʳ���Ҫ���е����·���Ƕ��٣�
��ͼ����һ��������ij��������߷ֱ��� 6��4��5���ڵ���A����һֻ���ϣ�����Ե�����������B����ʳ���Ҫ���е����·���Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com