
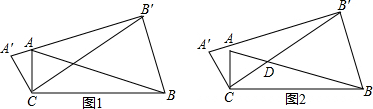
分析 (1)先利用互余计算出∠BAC=72°,再根据旋转的性质得到CA=CA′,∠BAC=∠A′=18°,∠ACA′=θ,然后根据等腰三角形的性质和三角形内角和计算出∠ACA′即可;
(2)根据旋转的性质得∠BCB′=θ,CB=CB′,则∠CB′B=∠CBB′,然后分类讨论:设∠BDB′=x,当BB′=BD时,利用等腰三角形的性质得∠BDB′=∠DBB′=x,则∠DBB′=∠CBB′=x+18°,再由三角形内角和得到x+x+x+18°=180°,解方程求出x后利用三角形外角性质求θ;当BB′=DB′时,利用前面的方法计算即可.
解答 解:(1)∵∠ACB=90°,∠ABC=18°,
∴∠BAC=90°-18°=72°,
∵△ABC绕顶点C逆时针旋转,旋转角为θ,得到△A′B′C,
∴CA=CA′,∠BAC=∠A′=18°,∠ACA′=θ,
∴∠CAA′=∠A′=72°,
∴∠ACA′=180°-2×72°=36°,
即θ的值为36°;
(2)∵△ABC绕顶点C逆时针旋转,旋转角为θ,得到△A′B′C,
∴∠BCB′=θ,CB=CB′,
∴∠CB′B=∠CBB′,
设∠BDB′=x,
当BB′=BD时,则∠BDB′=∠DBB′=x,
∴∠DBB′=∠CBB′=x+18°,
在△BDB′中,x+x+x+18°=180°,解得x=54°,
而∠BDB′=∠BCB′+∠CBD,
∴θ+18°=54°,解得θ=36°;
当BB′=DB′时,则∠BDB′=∠DB′D=∠CBB′=x,
∴∠DBB′=x-18°,
在△BDB′中,x+x+x-18°=180°,解得x=66°,
而∠BDB′=∠BCB′+∠CBD,
∴θ+18°=66°,解得θ=48°.
综上所述,θ的值为36°或48°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和三角形内角和.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6≤a≤-$\frac{11}{2}$ | B. | -6<a≤-$\frac{11}{2}$ | C. | -6<a<-$\frac{11}{2}$ | D. | -6≤a<-$\frac{11}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
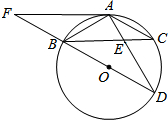 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式,并把解集表示在数轴上:$\left\{\begin{array}{l}{5x+7>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$.
解不等式,并把解集表示在数轴上:$\left\{\begin{array}{l}{5x+7>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
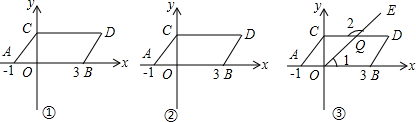
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com