
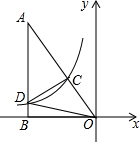
 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=-9.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=-9. 分析 作CE⊥OB于E,如图,根据反比例函数的比例系数k的几何意义得到S△OCE=S△BOD=$\frac{1}{2}$k,再根据三角形面积公式得到S△ACD=12,且OC=$\frac{1}{3}$OA,则S△OAB=36+$\frac{1}{2}$k,然后证明△OCE∽△OAB,利用相似三角形的性质即可得到k的值.
解答 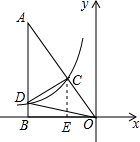 解:作CE⊥OB于E,如图,
解:作CE⊥OB于E,如图,
∵点C、D在双曲线y=$\frac{k}{x}$(x<0)上,
∴S△OCE=S△BOD=$\frac{1}{2}$k,
∵OC:AC=1:2,S△OCD=12,
∴S△ACD=24,OC=$\frac{1}{3}$OA,
∴S△OAB=36+$\frac{1}{2}$|k|,
∵CE∥AB,
∴△OCE∽△OAQB,
∴$\frac{{S}_{△OCE}}{{S}_{△OAB}}$=($\frac{OC}{OA}$)2,即$\frac{\frac{1}{2}•|k|}{36+\frac{1}{2}|k|}$=$\frac{1}{9}$,
∴k=±9.
∵k<0,
∴k=-9.
故答案为-9.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


科目:初中数学 来源: 题型:选择题
| A. | 1.5×106 | B. | 1.5×107 | C. | 1.5×108 | D. | 1.5×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “购买一张彩票就中奖”是不可能事件 | |
| B. | “抛掷一枚质地均匀的骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应做普查 | |
| D. | 从扇形统计图中,可以直接得到各部分的具体数值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
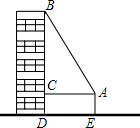 如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?
如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com