
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2﹣11x+24=0的两个根,D是AB上的点,且满足![]() .
.
(1)矩形OABC的面积是 ,周长是 .
(2)求直线OD的解析式;
(3)点P是射线OD上的一个动点,当△PAD是等腰三角形时,求点P的坐标.

【答案】(1)S=24,C=22;(2)y=-x;(3)P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0);  ;
; 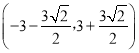
【解析】试题分析:(1)根据边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,即可得到AO=3,AB=8,进而得出矩形OABC的面积以及矩形OABC的周长;
(2)根据![]() ,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
(3)根据△PAD是等腰三角形,分情况讨论,根据等腰直角三角形的性质,求得点P的坐标.
试题解析:(1)(1)∵x2-11x+24=0,
∴(x-3)(x-8)=0,
∴x1=3,x2=8,
∵AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,
∴AO=3,AB=8,
∴矩形OABC的面积=3×8=24,矩形OABC的周长=2×(3+8)=22,
故答案为:24,22;
(2)∵![]() ,AB=8,
,AB=8,
∴AD=3,
又∵AO=3,
∴D(-3,3),
设直线OD解析式为y=kx,则
3=-3k,即k=-1,
∴直线OD的解析式为y=-x;
(3)∵AD=AO=3,∠DAO=90°,
∴△AOD是等腰直角三角形,
∴∠ADO=45°,DO=3![]() ,
,
根据△PAD是等腰三角形,分4种情况讨论:
①如图所示,当AD=AP1=3时,点P1的坐标为(0,0);
②如图所示,当DA=DP2=3时,过P2作x轴的垂线,垂足为E,则
OP2=3![]() -3,△OEP2是等腰直角三角形,
-3,△OEP2是等腰直角三角形,
∴P2E=OE=![]() =3-
=3-![]() ,
,
∴点P2的坐标为(-3+![]() ,3-
,3-![]() );
);
③如图所示,当AP3=DP3时,∠DAP3=∠ADO=45°,
∴△ADP3是等腰直角三角形,
∴DP3=![]() =
=![]()
∴P3O=3![]() -
-![]() =
=![]() ,
,
过P3作x轴的垂线,垂足为F,则△OP3F是等腰直角三角形,
∴P3F=OF=![]() ,
,
∴点P3的坐标为(-![]() ,
, ![]() );
);
④如图所示,当DA=DP4=3时,P4O=3+3![]() ,
,
过P4作x轴的垂线,垂足为G,则△OP4G是等腰直角三角形,
∴P4G=OG=![]() +3,
+3,
∴点P4的坐标为(-3-![]() ,3+
,3+![]() );
);
综上所述,P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0); ![]() ;
; ![]()



 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米![]() 小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
![]() 求BC间的距离;
求BC间的距离;![]() 这辆小汽车超速了吗?请说明理由.
这辆小汽车超速了吗?请说明理由.

【答案】这辆小汽车没有超速.
【解析】
(1)根据勾股定理求出BC的长;
(2)直接求出小汽车的时速,进行比较得出答案.
(1)在Rt△ABC中,AC=60 m,
AB=100 m,且AB为斜边,根据勾股定理,得BC=80 m.
(2)这辆小汽车没有超速.
理由:∵80÷5=16(m/s),
而16 m/s=57.6 km/h,57.6<70,
∴这辆小汽车没有超速.
【点睛】
考查勾股定理的应用,熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19
【题目】已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F是DG上一点,![]() ,且
,且![]() .
.
![]() 求证:
求证:![]() ;
;![]() 若
若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
第一次 | 第二次 | |
甲种货车的辆数 | 2辆 | 5辆 |
乙种货车的辆数 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
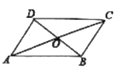
(1)求证:四边形ABCD是平行四边形
(2)若AC⊥BD,且AB=4,则四边形ABCD的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程
(1)25x2+10x+1=0(公式法) (2) 7x2 -23x +6=0;(配方法)
(3) ![]() (分解因式法) (4)x2-4x-396=0(适当的方法)
(分解因式法) (4)x2-4x-396=0(适当的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和 5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔 记本的价格分别是( )
A.0.8 元/支,2.6 元/本B.0.8 元/支,3.6 元/本
C.1.2 元/支,2.6 元/本D.1.2 元/支,3.6 元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“独立思考”所在的扇形的圆心角的度数为 度;
(3)请将条形统计图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:在菱形ABCD中,E、F分别是BC,CD上的点,且CE=CF.

(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com