
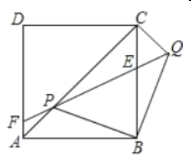
【题目】如图,正方形![]() 、等腰
、等腰![]() 的顶点
的顶点![]() 在对角线
在对角线![]() 上(点
上(点![]() 与
与![]() 、
、![]() 不重合),
不重合),![]() 与
与![]() 交于
交于![]() ,
,![]() 延长线与
延长线与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)求证:![]()
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)证出∠ABP=∠CBQ,由SAS证明△ABP≌△CBQ可得结论;
(2)根据正方形的性质和全等三角形的性质得到![]() ,∠APF=∠ABP,可证明△APF∽△ABP,再根据相似三角形的性质即可求解;
,∠APF=∠ABP,可证明△APF∽△ABP,再根据相似三角形的性质即可求解;
(3)根据全等三角形的性质得到∠BCQ=∠BAC=45°,可得∠PCQ=90°,根据三角函数和已知条件得到![]() ,由(2)可得
,由(2)可得![]() ,等量代换可得∠CBQ=∠CPQ即可求解.
,等量代换可得∠CBQ=∠CPQ即可求解.
(1)∵![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
(3)由(1)得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由(2)![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
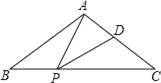
【题目】如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
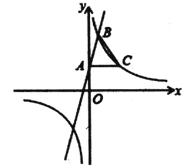
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第一象限内的图象交于点
在第一象限内的图象交于点![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 轴交反比例函数
轴交反比例函数![]() 的图象于点
的图象于点![]() ,连接
,连接![]() .
.
(1)求反比例函数的表达式.
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥轴于B且S△ABO =
在第二象限的交点,AB⊥轴于B且S△ABO =![]() .
.
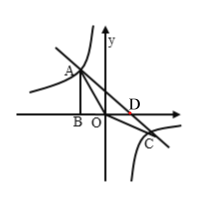
(1)求这两个函数的解析式.
(2)求直线与双曲线的两个交点A,C和直线AC与x轴的交点D的坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为![]() 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)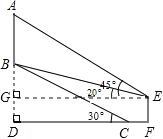
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.

求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
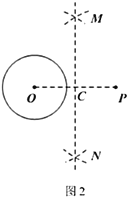
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
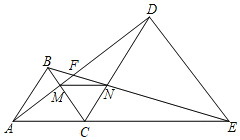
【题目】如图,![]() 和
和![]() 都是等边三角形,且点A、C、E在同一直线上,
都是等边三角形,且点A、C、E在同一直线上,![]() 与
与![]() 、
、![]() 分别交于点F、M,
分别交于点F、M,![]() 与
与![]() 交于点N.下列结论正确的是_______(写出所有正确结论的序号).
交于点N.下列结论正确的是_______(写出所有正确结论的序号).
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com