Question

18．定义，如果一个锐角等腰三角形满足一个角的2倍，那么我们称这个三角形为“智慧三角形”．
（1）“智慧三角形”顶角的度数为36°；
（2）如图1，正五边形ABCDE中，对角线AC，BE交于点P．求证：△APE为智慧三角形；
（3）如图2，六边形ABCDEF中，AB∥DE，BC∥EF，CD∥AF，且∠A=108°，∠B=144°，
①求∠D的度数；
②求证：AB+BC=DE+EF．

Answer 1

分析 （1）分两种情况：①底角度数是顶角度数的2倍时，设顶角度数为x，则底角度数为2x，由三角形内角和定理得出方程，解方程求出x即可；
②顶角度数是底角度数的2倍时，设底角度数为x，则顶角度数为2x，由三角形内角和定理得出方程，解方程求出x，得出2x=90°（不合题意）；即可得出结果；
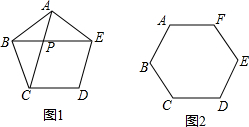
（2）由正五边形的性质得出AB=AE=BC，∠ABC=∠BAE=108°，得出∠ABE=∠AEB=∠ACB=36°，求出∠APE=∠PAE=2∠AEB，AE=PE，得出△APE为智慧三角形；
（3）①延长FA、CB交于点G，延长AB、DC交于点H，延长CD、FE交于M，求出∠G=72°，∠H=72°，由平行线的性质得出∠CDE=108°；
②证出BG=AB，同理：EM=DE，证明四边形GCMF是平行四边形，得出GC=FM，即可得出结论．

解答 （1）解：分两种情况：
①底角度数是顶角度数的2倍时，
设顶角度数为x，则底角度数为2x，
由三角形内角和定理得：x+2x+2x=180°，
解得：x=36°，即顶角度数为36°；
②顶角度数是底角度数的2倍时，
设底角度数为x，则顶角度数为2x，
由三角形内角和定理得：x+x+2x=180°，
解得：x=45°，2x=90°（不合题意）；
综上所述：“智慧三角形”顶角的度数为36°；
故答案为：36°；
（2）证明：∵五边形ABCDE是正五边形，
∴AB=AE=BC，∠ABC=∠BAE=108°，
∴∠ABE=∠AEB=∠ACB=36°，
∴∠PAE=108°-36°=72°，
∴∠APE=72°，
∴∠APE=∠PAE=2∠AEB，
∴AE=PE，
∴△APE为智慧三角形；
（3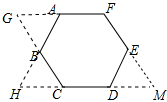）①解：延长FA、CB交于点G，延长AB、DC交于点H，延长CD、FE交于M，如图所示：
∵∠BAF=108°，∠ABC=144°，
∴∠BAG=72°，∠ABG=36°，
∴∠G=72°，
同理：∠H=72°，
∵AB∥DE，
∴∠CDE=180°-72°=108°；
②证明：∵∠G=∠BAG，
∴BG=AB，
同理：EM=DE，
∵BC∥EF，CD∥AF，
∴四边形GCMF是平行四边形，
∴GC=FM，
即BG+BC=EM+EF，
∴AB+BC=DE+EF．

点评 本题考查了“智慧三角形”的判定、正五边形的性质、平行线的性质、等腰三角形的判定与性质、平行四边形的判定与性质等知识；本题综合性强，有一定难度，特别是（3）中，需要通过作辅助线证明四边形是平行四边形才能得出结论．